Question

In Newton ring’s set up, when a drop of water is introduced between the lens and the glass slab then the rings;
A) Contracts
B) Expands
C) Remains the same
D) First expands then contract

Answer 1

Hint: Refraction of light and reflection of light both happen and the reflected and refracted ray get super imposed. This gives rise to the rings.

Complete step by step solution:
Newton’s ring test is a test used to determine the efficiency of a Plano convex lens. In this test light from a sodium lamp is reflected by a plain glass and made to fall normally on a Plano convex lens. The light undergoes refraction and we get a refracted light. Also, the lens is kept horizontal on a glass slab which is responsible for reflection of light. These reflected and refracted lights due to that very small volume between the glass slab and lens behave as waves and hence undergo interference.

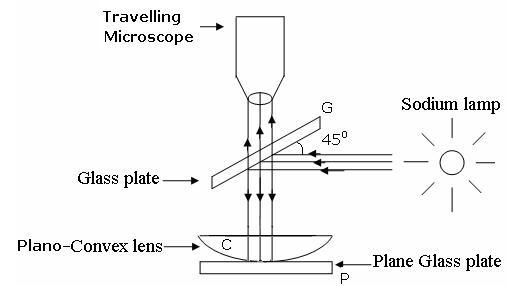
The above diagram shows the apparatus for Newton’s ring test.
The pattern is created by placing a very slightly convex curved glass on an optical flat glass. The two pieces of glass make contact only at the center, at other points there is a slight air gap between the two surfaces, increasing with radial distance from the center to the microscope. The diagram at right shows a small section of the two pieces, with the gap increasing right to left.
Light from a monochromatic (single color) source shines through the top piece and reflects from both the bottom surface of the top piece and the top surface of the optical flat, and the two reflected rays combine and superpose. However the ray reflecting off the bottom surface travels a longer path. The additional path length is equal to twice the gap between the surfaces. In addition the ray reflecting off the bottom piece of glass undergoes a ${180^ \circ }$ phase reversal, while the internal reflection of the other ray from the underside of the top glass causes no phase reversal. The brightness of the reflected light depends on the difference in the path length of the two rays:

Constructive interference:In areas where the path length difference between the two rays is equal to an odd multiple of half a wavelength $\dfrac{\lambda}{2}$ of the light waves, the reflected waves will be in phase, so the "troughs" and "peaks" of the waves coincide. Therefore, the waves will reinforce (add) and the resulting reflected light intensity will be greater. As a result, a bright area will be observed there.

Destructive interference: At other locations, where the path length difference is equal to an even multiple of a half-wavelength, the reflected waves will be ${180^ \circ }$ out of phase, so a "trough" of one wave coincides with a "peak" of the other wave. Therefore, the waves will cancel (subtract) and the resulting light intensity will be weaker or zero. As a result, a dark area will be observed there. Because of the ${180^ \circ }$ phase reversal due to reflection of the bottom ray, the center where the two pieces touch is dark.
Since the gap between the glasses increases radially from the center, the interference fringes form concentric rings. The thickness of the rings decreases as their diameter decreases. The brightness pattern is similar to a single slit interference pattern. The diagram below shows the interference pattern.

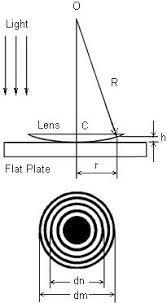
Now the medium between the lens and glass plate is air, so let’s say the diameter of ${n^{th}}$ ring in the case of air is ${d_n}$.
Now let the water drop be introduced between the lens and glass plate. The diameter of the glass plate will change. As the refractive index of water is different (more) than that of air, the diameters in both the mediums will be different. So, let the diameter of the ${n_{th}}$ ring be ${d'_n}$
So refractive index of water will be given by;
${\eta _{water}} = \dfrac{{{d_n}}}{{{{d'}_n}}}$---------🡪 (formula for refractive index)
Now, we know that, ${\eta _{water}} > 1$;
Hence, $\dfrac{{{d_n}}}{{{{d'}_n}}} > 1$.
Therefore, ${d_n} > {d'_n}$.
Thus, the diameter of the rings contract when a drop of water is introduced between the lens and the glass plate.

So, option A is correct.

Note:The refractive index is the ratio of quantity in air to the quantity in that medium.
Here, we have considered the definition of refractive index based on the height of the image.
Higher the refractive index lesser is the height of image.