
Let $\mathrm{B}_{\mathrm{P}}$ and $\mathrm{B}_{\mathrm{Q}}$ be the magnetic field produced by the wire $\mathrm{P}$ and $\mathrm{Q}$ which are placed symmetrically $\mathrm{i}$a rectangular loop ABCD as shown in figure. Current in wire $\mathrm{P}$ is directed inward and in $\mathrm{Q}$ is $2 \mathrm{I}$ directed outwards. if $\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{B}} \mathrm{Q} \cdot \overrightarrow{\mathrm{d}} \ell=2 \mu_{0}$ tesla meter $, \int_{\mathrm{D}}^{\mathrm{A}} \overrightarrow{\mathrm{B}} \mathrm{p} \cdot \overrightarrow{\mathrm{d}} \ell=-2 \mu_{0}$
tesla meter $\int_{\mathbf{A}}^{\mathbf{B}}{\overrightarrow{{{\mathbf{B}}_{\mathbf{P}}}}}\cdot \overrightarrow{\mathbf{d}\ell }=-{{\mu }_{0}}$ tesla meter the value of I will be:
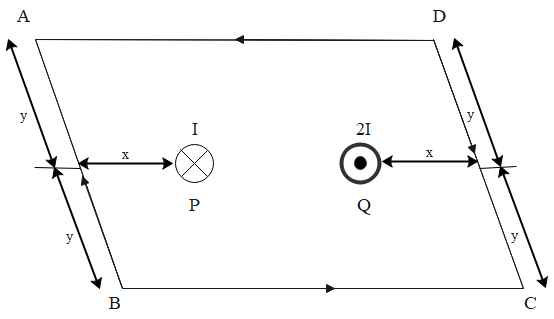
(A) 8 A
(B) 4 A
(C) 5 A
(D) 6 A
Answer
133.5k+ views
Hint: We know that the magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetized materials. A charge that is moving in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. The magnetic field is generated by electric currents due to the motion of convection currents of a mixture of molten iron and nickel in the Earth's outer core: these convection currents are caused by heat escaping from the core, a natural process called a geodynamic.
Complete step by step answer
We know that the principle of superposition states that every charge in space creates an electric field at a point independent of the presence of other charges in that medium. The resultant electric field is a vector sum of the electric field due to individual charges. The principle of superposition may be applied to waves whenever two (or more) waves travelling through the same medium at the same time. The waves pass through each other without being disturbed. The net displacement of the medium at any point in space or time, is simply the sum of the individual wave displacements.
$P \rightarrow A B, C D, D A, B C$
$Q \rightarrow A B, C D, D A, B C$
Given $\int_{A}^{B} \vec{B}_{Q} \cdot d \vec{l}=2 \mu_{0} T-m$
$\int_{D}^{B} \vec{B}_{P} \cdot d \vec{l}=-2 \mu_{0} T-m$
$\int_{A}^{B} \vec{B}_{P} \cdot d \vec{l}=-\mu_{0} T-m$
we know $\int \vec{B}_{n e t} \cdot D \vec{l}=\mu_{0}(2 I-I)=\mu_{0} I$
Using superposition taking wire $\mathrm{P}$ only $\int \vec{B}_{P} \cdot d \vec{l}=-\mu_{0} I$ and $\int \vec{B}_{Q} \cdot d \vec{l}=\mu_{0} 2 I$
$\int_{A}^{B} \vec{B}_{P} d \vec{l}+\int_{B}^{C} \vec{B}_{P} d \vec{l}+\int_{A}^{D} \vec{B}_{P} d \vec{l}+\int_{D}^{A} \vec{B}_{P} d \vec{l}=-\mu_{0} I$
From symmetry it is clear $\int_{B}^{C} \vec{B}_{P} d \vec{l}=\int_{D}^{A} \vec{B}_{P} d \vec{l}$
$\operatorname{As} \int_{A}^{B} \vec{B}_{Q} d \vec{l}=2 \mu_{0} I$
Hence, $\int_{B}^{C} \vec{B}_{P} d \vec{l}=-\mu_{0} I$
Also, $\int_{D}^{A} \vec{B}_{Q} d \vec{l}=-2 \mu_{0} I$
Then, $\int_{A}^{D} \vec{B}_{Q} d \vec{l}=4 \mu_{0} I=\int \vec{B}_{Q} d \vec{l}$
$\int_{A}^{B} \vec{B}_{P} d \vec{l}=-\mu_{0} I \Rightarrow \int_{D}^{C} \vec{B}_{Q} d \vec{l}=2 \mu_{0} I$
$\int \vec{B}_{\text {net }} d \vec{l}=\int \vec{B}_{P} d \vec{l}+\int \vec{B}_{Q} d \vec{l}=\mu_{0} I$
$=\left[-\mu_{0} I-\mu_{0} I-2 \mu_{0} I-2 \mu_{0} I\right]$
$+\left[2 \mu_{0} I+2 \mu_{0} I+4 \mu_{0} I+4 \mu_{0} I\right]$
$=-6 \mu_{0} I+12 \mu_{0} I=\mu_{0}(6 I)$
Hence, $I=6 A .$
So option D is correct.
Note:
We know that the superposition theorem states that for a linear system (notably including the subcategory of time-invariant linear systems) the response (voltage or current) in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source. The application of superposition theorem is, we can employ only for linear circuits as well as the circuit which has more supplies. Equivalent section currents and voltages algebraically included discovering what they will perform with every power supply in effect. The total current in any part of a linear circuit equals the algebraic sum of the currents produced by each source separately. To evaluate the separate currents to be combined, replace all other voltage sources by short circuits and all other current sources by open circuits.
Complete step by step answer
We know that the principle of superposition states that every charge in space creates an electric field at a point independent of the presence of other charges in that medium. The resultant electric field is a vector sum of the electric field due to individual charges. The principle of superposition may be applied to waves whenever two (or more) waves travelling through the same medium at the same time. The waves pass through each other without being disturbed. The net displacement of the medium at any point in space or time, is simply the sum of the individual wave displacements.
$P \rightarrow A B, C D, D A, B C$
$Q \rightarrow A B, C D, D A, B C$
Given $\int_{A}^{B} \vec{B}_{Q} \cdot d \vec{l}=2 \mu_{0} T-m$
$\int_{D}^{B} \vec{B}_{P} \cdot d \vec{l}=-2 \mu_{0} T-m$
$\int_{A}^{B} \vec{B}_{P} \cdot d \vec{l}=-\mu_{0} T-m$
we know $\int \vec{B}_{n e t} \cdot D \vec{l}=\mu_{0}(2 I-I)=\mu_{0} I$
Using superposition taking wire $\mathrm{P}$ only $\int \vec{B}_{P} \cdot d \vec{l}=-\mu_{0} I$ and $\int \vec{B}_{Q} \cdot d \vec{l}=\mu_{0} 2 I$
$\int_{A}^{B} \vec{B}_{P} d \vec{l}+\int_{B}^{C} \vec{B}_{P} d \vec{l}+\int_{A}^{D} \vec{B}_{P} d \vec{l}+\int_{D}^{A} \vec{B}_{P} d \vec{l}=-\mu_{0} I$
From symmetry it is clear $\int_{B}^{C} \vec{B}_{P} d \vec{l}=\int_{D}^{A} \vec{B}_{P} d \vec{l}$
$\operatorname{As} \int_{A}^{B} \vec{B}_{Q} d \vec{l}=2 \mu_{0} I$
Hence, $\int_{B}^{C} \vec{B}_{P} d \vec{l}=-\mu_{0} I$
Also, $\int_{D}^{A} \vec{B}_{Q} d \vec{l}=-2 \mu_{0} I$
Then, $\int_{A}^{D} \vec{B}_{Q} d \vec{l}=4 \mu_{0} I=\int \vec{B}_{Q} d \vec{l}$
$\int_{A}^{B} \vec{B}_{P} d \vec{l}=-\mu_{0} I \Rightarrow \int_{D}^{C} \vec{B}_{Q} d \vec{l}=2 \mu_{0} I$
$\int \vec{B}_{\text {net }} d \vec{l}=\int \vec{B}_{P} d \vec{l}+\int \vec{B}_{Q} d \vec{l}=\mu_{0} I$
$=\left[-\mu_{0} I-\mu_{0} I-2 \mu_{0} I-2 \mu_{0} I\right]$
$+\left[2 \mu_{0} I+2 \mu_{0} I+4 \mu_{0} I+4 \mu_{0} I\right]$
$=-6 \mu_{0} I+12 \mu_{0} I=\mu_{0}(6 I)$
Hence, $I=6 A .$
So option D is correct.
Note:
We know that the superposition theorem states that for a linear system (notably including the subcategory of time-invariant linear systems) the response (voltage or current) in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the responses caused by each independent source. The application of superposition theorem is, we can employ only for linear circuits as well as the circuit which has more supplies. Equivalent section currents and voltages algebraically included discovering what they will perform with every power supply in effect. The total current in any part of a linear circuit equals the algebraic sum of the currents produced by each source separately. To evaluate the separate currents to be combined, replace all other voltage sources by short circuits and all other current sources by open circuits.
Recently Updated Pages
JEE Main 2025 Session 2 Form Correction (Closed) – What Can Be Edited

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main Books 2023-24: Best JEE Main Books for Physics, Chemistry and Maths

JEE Main 2023 April 13 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 11 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 10 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Wheatstone Bridge for JEE Main Physics 2025

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Diffraction of Light - Young’s Single Slit Experiment

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

If a wire of resistance R is stretched to double of class 12 physics JEE_Main

JEE Advanced 2024 Syllabus Weightage

Current Loop as Magnetic Dipole and Its Derivation for JEE




