




Series vs Parallel Capacitor Combination: Key Differences and Calculations
A combination of capacitors describes the method by which multiple capacitors are connected in an electrical circuit to achieve desired overall capacitance and electrical properties. These connections play a significant role in controlling charge storage, voltage distribution, and circuit behaviour, especially in applications relevant to JEE Main Physics.
Concept of Combination of Capacitors
Capacitors can be combined in series, parallel, or as a mix of both, depending on circuit requirements. The total capacitance resulting from such combinations determines how a circuit manages charge and voltage.
The arrangement of capacitors affects the equivalent capacitance, voltage across each unit, and the distribution of charge. Capacitor networks are simplified step-by-step by identifying pure series or parallel groups before reducing mixed configurations.
Understanding capacitor combinations is foundational before studying advanced topics such as Intro To Electrostatics and RC circuits. This topic also enables precise control of energy storage and timing features in both theoretical and practical circuits.
Series Combination of Capacitors
In a series arrangement, capacitors are linked end to end so that the same charge flows through each capacitor, but the total potential difference is divided among them. The total or equivalent capacitance of capacitors in series is always less than the smallest individual capacitance in the group.
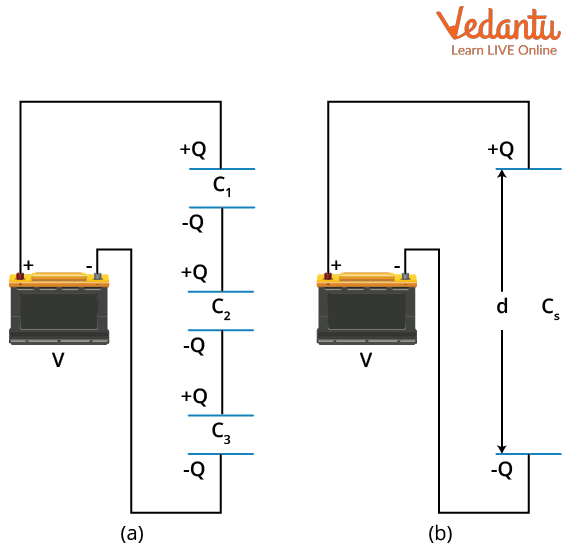
For $n$ capacitors in series, labeled $C_1, C_2, \ldots, C_n$, the equivalent capacitance $C_{eq}$ is given by the formula:
$\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \ldots + \dfrac{1}{C_n}$
In this configuration, the charge $Q$ on each capacitor is equal. The voltages across individual capacitors add to the total applied voltage, so $V = V_1 + V_2 + \ldots + V_n$.
- Same charge on each capacitor
- Sum of potential differences equals total voltage
- Equivalent capacitance is reduced
Parallel Combination of Capacitors
Capacitors in parallel are connected such that their plates of like polarity are joined. In this arrangement, all capacitors experience the same potential difference across their terminals, but the total charge stored is divided among the capacitors according to their capacitances.
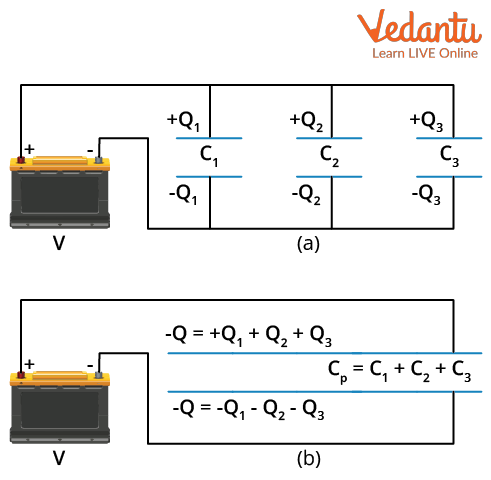
For $n$ capacitors in parallel, the equivalent capacitance $C_{eq}$ is calculated as:
$C_{eq} = C_1 + C_2 + \ldots + C_n$
The total charge stored is the sum of charges on each capacitor: $Q = Q_1 + Q_2 + \ldots + Q_n$. The potential difference across each capacitor is equal to the applied voltage $V$.
- Same voltage across each capacitor
- Charge is divided among capacitors
- Equivalent capacitance increases
Comparison of Series and Parallel Combinations
The effect of series and parallel arrangements on key capacitor properties can be understood by comparing voltage, charge, and net capacitance as shown below.
| Property | Series Combination | Parallel Combination |
|---|---|---|
| Equivalent Capacitance | $\dfrac{1}{C_{eq}} = \sum \dfrac{1}{C_i}$ | $C_{eq} = \sum C_i$ |
| Charge | Same on each ($Q$) | Divided according to $C_i$ |
| Voltage | Divided among capacitors | Same across all |
| Resulting $C_{eq}$ | Less than smallest $C$ | Greater than largest $C$ |
Solving Mixed Combinations of Capacitors
Mixed combinations involve both series and parallel arrangements in the same network. Identifying and reducing pure series or parallel groups stepwise allows for calculation of total equivalent capacitance. Use the respective formula at each reduction stage.
When dealing with complex circuits, redraw the network to highlight clear groups and ensure no capacitors are incorrectly labeled. Always use SI units for capacitance values for accuracy in competitive exams.
Related concepts are explored in Basics Of Current Electricity and capacitor charging concepts in What Is An RC Circuit.
Stepwise Derivation and Formulas
For series, apply Kirchhoff’s law on potential differences to derive the series formula, keeping in mind that charge remains constant. In parallel, combine the charges across each capacitor since voltage is constant. The stepwise approach prevents calculation errors.
Correct application of the reciprocals in series and direct summation in parallel is essential for solving numerical problems involving combined capacitors.
Solved Example: Combination of Capacitors
Three capacitors with values $C_1 = 2~\mu\text{F}$, $C_2 = 3~\mu\text{F}$, and $C_3 = 6~\mu\text{F}$ are connected in series. To find the equivalent capacitance $C_{eq}$:
$\dfrac{1}{C_{eq}} = \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{6} = \dfrac{3+2+1}{6} = 1$
Therefore, $C_{eq} = 1~\mu\text{F}$, demonstrating that equivalent capacitance in series is less than any individual value.
Energy Stored in Capacitor Combinations
The energy stored by a capacitor is given by $U = \dfrac{1}{2} C V^2$, where $C$ is either the individual or the equivalent capacitance, and $V$ is the applied voltage. In combinations, use $C_{eq}$ to determine total stored energy.
For series arrangements, less energy is stored for the same applied voltage compared to the parallel combination, due to the smaller equivalent capacitance obtained in series.
Applications of Capacitor Combinations
Capacitor combinations are used to design circuits with specific capacitance values, voltage ratings, and energy storage requirements. These are fundamental in signal filtering, timing circuits, and voltage smoothing in power supplies.
Common Mistakes and Key Points
- Incorrectly identifying series and parallel groups
- Errors in reciprocals for series combinations
- Not converting units to Farads in calculations
- Ignoring capacitor voltage limitations
- Assuming rules of resistors and capacitors are identical
Related Topics and Further Study
A clear understanding of capacitor combinations enhances conceptual clarity in advanced circuits, energy calculations, and electric potential. Students are encouraged to explore Understanding Electric Potential for a broader perspective.
Detailed problems and practice examples can be found in the dedicated Combination Of Capacitors resource for further mastery relevant to JEE Main Physics.
FAQs on Understanding How Capacitors Combine in Circuits
1. What is the combination of capacitors?
Combination of capacitors refers to connecting two or more capacitors together to achieve a desired total capacitance in a circuit. There are mainly two ways to combine capacitors:
- Series combination: The reciprocal of total capacitance equals the sum of reciprocals of individual capacitances.
- Parallel combination: The total capacitance is the sum of all individual capacitances.
2. What happens when capacitors are connected in series?
When capacitors are connected in series, the overall or equivalent capacitance decreases and is always less than the smallest individual capacitor. The formula is:
- 1/Ceq = 1/C1 + 1/C2 + ...
3. What happens when capacitors are connected in parallel?
When capacitors are connected in a parallel combination, the total capacitance increases and is equal to the sum of all individual capactances:
- Ceq = C1 + C2 + ...
4. Why do we combine capacitors in a circuit?
We combine capacitors to achieve required capacitance values and voltage ratings for specific circuit needs. This allows:
- Tuning circuits to a desired frequency
- Storing more or less charge as required
- Increasing the voltage endurance by connecting in series or total capacitance by connecting in parallel
5. How do you calculate the effective capacitance in series and parallel combinations?
Effective capacitance can be found using specific formulas for both combinations:
- For series: 1/Ceq = 1/C1 + 1/C2 + ...
- For parallel: Ceq = C1 + C2 + ...
6. What are the applications of series and parallel combinations of capacitors?
Series and parallel combinations of capacitors are used for different purposes:
- Series: To handle higher voltages by increasing the voltage rating across the combination.
- Parallel: To increase the total capacitance so that more electric charge can be stored.
7. Can you explain with an example how two capacitors are combined in series?
If you connect two capacitors, for example, 4 μF and 6 μF, in series:
- Use the formula: 1/Ceq = 1/4 + 1/6 = (3 + 2)/12 = 5/12
- Ceq = 12/5 = 2.4 μF
8. Can you explain with an example how two capacitors are combined in parallel?
When 6 μF and 8 μF capacitors are connected in parallel:
- Ceq = 6 + 8 = 14 μF
9. What is the formula for the equivalent capacitance when n identical capacitors are connected in series?
For n identical capacitors of capacitance C connected in series, the formula is:
- Ceq = C / n
10. Why does the equivalent capacitance decrease in a series combination but increase in a parallel combination?
In a series combination, the charge stored is the same, but the voltage is divided, causing the total or equivalent capacitance to decrease. In a parallel combination, each capacitor can store charge independently at the same voltage, so the capacitances add up, increasing the total capacitance.
- Series: Ceq less than individual capacitances
- Parallel: Ceq greater than individual capacitances

































