Answer
Verified89.7k+ views
Hint:In this problem, to determine the hydrogen-like atom $X$ that makes a transition to ${n^{th}}$ orbit from the second excited state, we have to evaluate the energy released during the transition of hydrogen and since the same energy is absorbed by $X$ during its transition (that is released before) therefore, we can compare the energies obtained during the two transitions to get the correct solution.
Formula used:
The formula used in this problem is of the energy obtained due to the transition between two energy levels which is given as: -
$E = - 13.6{Z^2}\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)$
Here, ${n_1}{\text{ }}and{\text{ }}{n_2}$ are the principal quantum numbers for high energy level and low energy level respectively.
Complete step by step solution:
We know that the expression for obtaining energy during the transition between two energy levels can be stated as: -
$E = - 13.6{Z^2}\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(1)$
It is given that the photon radiated from hydrogen $(Z = 1)$ corresponding to the second line of the Lyman series. Therefore, the transition will be from ${n_1} = 3$ to ${n_2} = 1$ as shown in the figure:
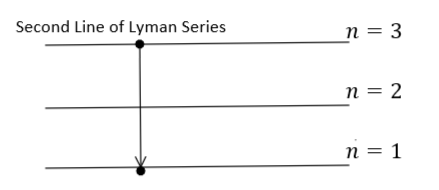
During this transition, the energy will be released which can be calculated using equation $(1)$ as: -
${E_{released}} = - 13.6{\left( 1 \right)^2}\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right) = - 13.6\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(2)$
$ \Rightarrow {E_{released}} = - 13.6\left( {\dfrac{1}{9} - \dfrac{1}{1}} \right) = 13.6\left( {\dfrac{8}{9}} \right)\,eV \\ $
Now, the same amount of energy is absorbed by a hydrogen-like atom $X\,(Z = Z)$ in the second excited state that makes a transition to ${n^{th}}$ orbit $(say\,{n_o})$ as described with the help of below-given diagram: -
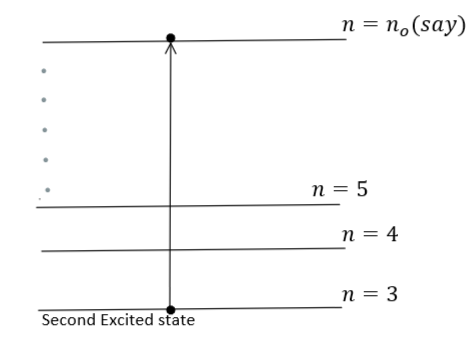
During this transition, the energy is absorbed. Therefore, using equation $(1)$, we get
${E_{absorbed}} = - 13.6{\left( Z \right)^2}\left( {\dfrac{1}{{{n_o}^2}} - \dfrac{1}{{{3^2}}}} \right) = - 13.6\left( {\dfrac{{{Z^2}}}{{{n_o}^2}} - \dfrac{{{Z^2}}}{{{3^2}}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(3)$
As the energy absorbed by hydrogen-like atom $X$ is same as the energy released by hydrogen hence, on comparing equations $(2)$ and $(3)$ , we get
${E_{released}} = {E_{absorbed}}$
$\Rightarrow - 13.6\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right) = - 13.6\left( {\dfrac{{{Z^2}}}{{{n_o}^2}} - \dfrac{{{Z^2}}}{{{3^2}}}} \right)$
On comparing both the sides, we get
$\dfrac{1}{{{3^2}}} = \dfrac{{{Z^2}}}{{{n_o}^2}}\,\,and\,\,\dfrac{1}{{{1^2}}} = \dfrac{{{Z^2}}}{{{3^2}}}$
$\Rightarrow \dfrac{1}{3} = \dfrac{Z}{{{n_o}}}\,\,and\,\,1 = \dfrac{Z}{3}$
Simplifying both the equations, we get $Z = 3$ and ${n_o} = 9$. Thus, the hydrogen-like atom $X$ is Lithium ion $L{i^{ + + }}(Z = 3)$ that makes a transition to ${9^{th}}$ orbit from second excited state i.e., $X = L{i^{ + + }},\,\,n = 9$.
Hence, the correct option is D.
Note: In this kind of problem, we can answer the problem by using the concept of $\dfrac{Z}{n}$ ratio like it is given that energy released in transition of hydrogen is same as that of energy absorbed in the transition of hydrogen-like atom and since transition of hydrogen is from ${n_1} = 3$ to ${n_2} = 1$ , then $3 \to 1$ transition in $H$ would give same energy as the $3 \times 3 \to 1 \times 3$ transition in $L{i^{ + + }}$ to main same $\dfrac{Z}{n}$ ratio.
Formula used:
The formula used in this problem is of the energy obtained due to the transition between two energy levels which is given as: -
$E = - 13.6{Z^2}\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)$
Here, ${n_1}{\text{ }}and{\text{ }}{n_2}$ are the principal quantum numbers for high energy level and low energy level respectively.
Complete step by step solution:
We know that the expression for obtaining energy during the transition between two energy levels can be stated as: -
$E = - 13.6{Z^2}\left( {\dfrac{1}{{n_1^2}} - \dfrac{1}{{n_2^2}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(1)$
It is given that the photon radiated from hydrogen $(Z = 1)$ corresponding to the second line of the Lyman series. Therefore, the transition will be from ${n_1} = 3$ to ${n_2} = 1$ as shown in the figure:
During this transition, the energy will be released which can be calculated using equation $(1)$ as: -
${E_{released}} = - 13.6{\left( 1 \right)^2}\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right) = - 13.6\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(2)$
$ \Rightarrow {E_{released}} = - 13.6\left( {\dfrac{1}{9} - \dfrac{1}{1}} \right) = 13.6\left( {\dfrac{8}{9}} \right)\,eV \\ $
Now, the same amount of energy is absorbed by a hydrogen-like atom $X\,(Z = Z)$ in the second excited state that makes a transition to ${n^{th}}$ orbit $(say\,{n_o})$ as described with the help of below-given diagram: -
During this transition, the energy is absorbed. Therefore, using equation $(1)$, we get
${E_{absorbed}} = - 13.6{\left( Z \right)^2}\left( {\dfrac{1}{{{n_o}^2}} - \dfrac{1}{{{3^2}}}} \right) = - 13.6\left( {\dfrac{{{Z^2}}}{{{n_o}^2}} - \dfrac{{{Z^2}}}{{{3^2}}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\,(3)$
As the energy absorbed by hydrogen-like atom $X$ is same as the energy released by hydrogen hence, on comparing equations $(2)$ and $(3)$ , we get
${E_{released}} = {E_{absorbed}}$
$\Rightarrow - 13.6\left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right) = - 13.6\left( {\dfrac{{{Z^2}}}{{{n_o}^2}} - \dfrac{{{Z^2}}}{{{3^2}}}} \right)$
On comparing both the sides, we get
$\dfrac{1}{{{3^2}}} = \dfrac{{{Z^2}}}{{{n_o}^2}}\,\,and\,\,\dfrac{1}{{{1^2}}} = \dfrac{{{Z^2}}}{{{3^2}}}$
$\Rightarrow \dfrac{1}{3} = \dfrac{Z}{{{n_o}}}\,\,and\,\,1 = \dfrac{Z}{3}$
Simplifying both the equations, we get $Z = 3$ and ${n_o} = 9$. Thus, the hydrogen-like atom $X$ is Lithium ion $L{i^{ + + }}(Z = 3)$ that makes a transition to ${9^{th}}$ orbit from second excited state i.e., $X = L{i^{ + + }},\,\,n = 9$.
Hence, the correct option is D.
Note: In this kind of problem, we can answer the problem by using the concept of $\dfrac{Z}{n}$ ratio like it is given that energy released in transition of hydrogen is same as that of energy absorbed in the transition of hydrogen-like atom and since transition of hydrogen is from ${n_1} = 3$ to ${n_2} = 1$ , then $3 \to 1$ transition in $H$ would give same energy as the $3 \times 3 \to 1 \times 3$ transition in $L{i^{ + + }}$ to main same $\dfrac{Z}{n}$ ratio.
Recently Updated Pages
Name the scale on which the destructive energy of an class 11 physics JEE_Main
Write an article on the need and importance of sports class 10 english JEE_Main
Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main
Choose the one which best expresses the meaning of class 9 english JEE_Main
What does a hydrometer consist of A A cylindrical stem class 9 physics JEE_Main
A motorcyclist of mass m is to negotiate a curve of class 9 physics JEE_Main