Question

Two bodies of masses 1 kg and 4 kg are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency 25 rad/s, and amplitude 1.6 cm while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take $g = 10m/{s^2}$)


(A). 20 N
(B). 10 N
(C). 60 N
(D). 40 N

Answer 1

Hint: The total force on the ground is due the two masses and the force due to Hooke’s law. We know the frequency of oscillation of smaller mass from which we can calculate the value of spring constant using the time period equation of a spring mass system.

Formula used:
Time period of oscillation of a spring mass system is given as
$T = 2\pi \sqrt {\dfrac{m}{k}} {\text{ }}...{\text{(i)}}$
where m signifies the mass of the oscillating body and k denotes the spring constant.
Hooke’s law is given as
$F = - kx$
where F is the restoring force and x denotes the displacement due to spring of spring constant k.

Complete step-by-step answer:
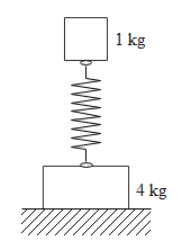
We are given two masses whose values are
$
  M = 4kg \\
  m = 1kg \\
$
They are attached through a spring. Let its spring constant is k. Smaller mass is oscillating with frequency given as
$\omega = 25rad/s$
We know the time period of oscillation for a spring-mass system given by equation (i). We can rewrite the equation using
$T = \dfrac{{2\pi }}{\omega }$
In the following way
$
  \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{m}{k}} \\
   \Rightarrow \dfrac{1}{\omega } = \sqrt {\dfrac{m}{k}} \\
$
The smaller mass is oscillating, so we substitute the known values and get
$
  \dfrac{1}{{25}} = \sqrt {\dfrac{1}{k}} \\
   \Rightarrow \sqrt k = 25 \\
$
Squaring both sides, we get
$k = 625N/m$
Now the maximum force exerted by the system on the floor is due to the two masses and the restoring force due to Hooke’s law given as
$F = Mg - \left( { - kx} \right) + mg{\text{ }}...{\text{(iii)}}$
The value of amplitude is given as
$x = 1.6cm = 0.016m$
Now substituting all the known values in equation (iii), we get
$
  F = 4 \times 10 + 625 \times 0.016 + 1 \times 10 \\
   = 40 + 10 + 10 \\
   = 60N \\
$
The correct answer is option C.

Note: 1. The Hooke’s law has negative signs because the restoring force always acts in the direction opposite to the applied force.
2. The restoring force is subtracted in expression for total force because this force is acting in the upward direction opposite to the weight of the smaller mass.