
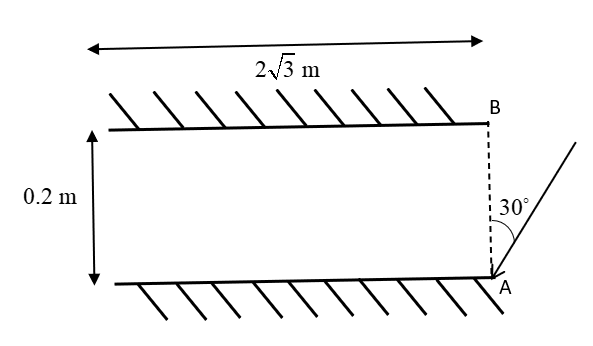
Two plane mirrors A and B are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle of ${30^ \circ }$ at a point just inside one end of A. The plane of incidence coincides with the plane of the figure. What is the maximum number of times the ray undergoes reflection (including the first one) before it emerges out?
A. 28
B. 30
C. 32
D. 34
Answer
218.4k+ views
Hint: The total distance that the ray will cover before emerging out will be equivalent to the length of the plane mirrors. To solve the above question, first calculate the distance that the ray will cover in one reflection and then proceed further to calculate the maximum number of reflections.
Complete answer:
The length of the mirrors is the distance that the ray should cover in order to emerge out.
Separation between the mirrors, $d = 0.2{\text{ m}}$
Let us calculate the distance that the ray covers in the first reflection.
For plane mirrors, the angle of incidence is equivalent to the angle of reflection.
Hence, angle of reflection $ = {30^ \circ }$ .
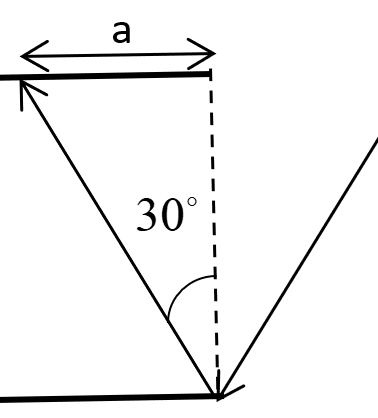
In the above triangle,
$\tan {30^ \circ } = \dfrac{a}{d}$
Substituting the values,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{a}{{0.2}}$
This gives $a = \dfrac{{0.2}}{{\sqrt 3 }}$
First reflection onwards, the distance covered by each ray would be $\dfrac{{0.2}}{{\sqrt 3 }}$ .
Let the total number of times the ray was reflected including the first one be $n$ , then
$n\left( {\dfrac{{0.2}}{{\sqrt 3 }}} \right) = 2\sqrt 3 $
On simplifying, we get $n = 30$ .
Hence, the maximum number of times the ray undergoes reflection before it emerges is 30.
Thus, the correct option is B.
Note:Angle of incidence is the angle that the incident ray makes with the normal of the mirror and angle of reflection is the angle that the reflected ray makes with the normal of the mirror. In the case of plane mirrors, the angle of incidence is equivalent to the angle of reflection. Use this property of plane mirrors and trigonometric relations to solve the given question.
Complete answer:
The length of the mirrors is the distance that the ray should cover in order to emerge out.
Separation between the mirrors, $d = 0.2{\text{ m}}$
Let us calculate the distance that the ray covers in the first reflection.
For plane mirrors, the angle of incidence is equivalent to the angle of reflection.
Hence, angle of reflection $ = {30^ \circ }$ .

In the above triangle,
$\tan {30^ \circ } = \dfrac{a}{d}$
Substituting the values,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{a}{{0.2}}$
This gives $a = \dfrac{{0.2}}{{\sqrt 3 }}$
First reflection onwards, the distance covered by each ray would be $\dfrac{{0.2}}{{\sqrt 3 }}$ .
Let the total number of times the ray was reflected including the first one be $n$ , then
$n\left( {\dfrac{{0.2}}{{\sqrt 3 }}} \right) = 2\sqrt 3 $
On simplifying, we get $n = 30$ .
Hence, the maximum number of times the ray undergoes reflection before it emerges is 30.
Thus, the correct option is B.
Note:Angle of incidence is the angle that the incident ray makes with the normal of the mirror and angle of reflection is the angle that the reflected ray makes with the normal of the mirror. In the case of plane mirrors, the angle of incidence is equivalent to the angle of reflection. Use this property of plane mirrors and trigonometric relations to solve the given question.
Recently Updated Pages
Young’s Double Slit Experiment Derivation Explained

Wheatstone Bridge Explained: Working, Formula & Uses

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding Average and RMS Value in Electrical Circuits




