Knowing About Degree and Radian Measure
In Geometry, angles are measured using two different units: degrees and radians. The numerical numbers for travelling "one round" of a circle equals 360 degrees or 2π radians. The degree, denoted by the symbol (°), is the most extensively used and well-known unit for measuring angles. Another angle measurement unit in geometry is called a radian, in short Rad. When determining the angles of trigonometric or periodic functions, radians are usually taken into account.
In this article, we will study how to convert into radian measure as well as several solved problems to convert into radians using the conversion formula. So, let's start by discussing what degrees and radians are.
What is Degree Measure?
A full 360-degree rotation defines a unit of angular measurement known as a degree, denoted by the symbol °. One degree is equal to π/180 radians since a full revolution equals 2π radians. As an alternative to utilising the decimal form, degrees can alternatively be stated using minutes and seconds. Prime (′) and double-prime (′′) letters are used to denote minutes and seconds.
1° = 0.017453 radians
What is Radian Measure?
To comprehend the radian measure or radian (Rad), we must first talk about central angles, which are angles with their vertex in the centre of a circle. The length of the corresponding arc, which is equal to the radius, is used to calculate the radian of a central angle. In other words, when the radius is curved around the circumference of a circle, the angle measured by the resulting arc is called a radian. Look at the example below.
1 radian = 57.2958°.
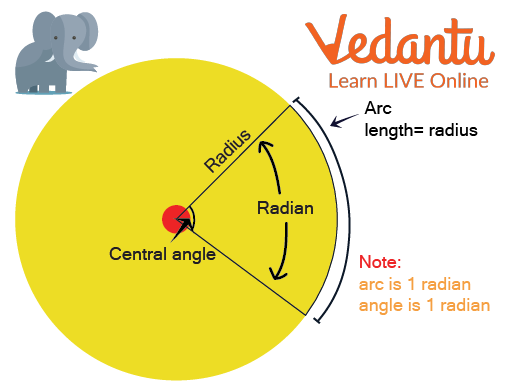
Radian Measure
Convert into Radian Formula
The formula for converting degrees to radians is a more general formula that may be used to change a given value in degrees to a value in radians and vice versa.
Radians = Degrees × π/180
Degrees to Radian Conversion Formula
How to Convert 60 Degrees into Radian?
The steps listed below demonstrate how to convert 60 degrees into radians:
Step 1: Write the number of degrees that you want to convert to radians, i.e 60.
Step 2: To convert from degrees to radians, multiply the number of degrees, i.e. 60 by π/180.
Step 3: Since your answer would be in radians, you can remove the degree sign.
Step 4: Simplify the expression obtained, i.e.
60 × π/180 = π/3.
Thus, the angle measurement in radians will be π/3 on simplification.
Note: The same procedure used to convert positive degrees into radians is applied to convert negative degrees. Simply multiply the angle's value given in degrees by π /180.
Solved Problems to Convert into Radian
Example 1: Convert into radian measure, 200 degrees.
Ans: We are aware of the formula.
Angle in radians = Angle in degree × π/180
Therefore, 200 degrees in radians are
= 200 × π/180
= 10π/9
= 3.491 Rad.
Example 2: In one minute, a wheel completes 360 revolutions. How many radians does it rotate around in a second?
Ans: It is given that the wheel does 360 total revolutions in a minute.
1 second = 360/60 = 6 revolutions
The fact that a wheel travels 2π radians in its single rotation. It will rotate a 360 x 2π radian =720π radian in a minute
Then in one second, it will turn an angle of
720π radian/60 = 12π radian
Therefore, the wheel makes a 12π radian turn in one second.
Practice Problems
1. Convert into radian measure: 700⁰
Ans. 12.21 Rad.
2. Determine the radians equivalent to 450 degrees.
Ans. 7.854 Rad.
3. Convert into radian measure, -300°.
Ans. -5.23 Rad.
Summary
We have discussed above, the two ways to measure the angle of a circle: in degrees and radians. We may convert between the two using formulae. Two rad or 360° are the same as one full circle. One radian (rad) equals 57.2958 degrees, and one degree is equal to 0.017453 radians (rad). An angle is multiplied by π/180⁰ to convert it from degrees to radians. This article has also covered how to convert 60° into radians. Try to solve the practice problems provided in this article using the degrees into radians conversion formula.
FAQs on Degrees into Radian
1. Why are radians more effective in the real world than degrees?
Radians and degrees both can be used to measure angles. Mathematicians most frequently prefer to use radians in place of degrees. Calculating the size of a circle's sector, the length of an arc, and the angular velocity can all be done using radian measurements. When dealing with the circular motion of an object, it is imperative to always use radians.
2. Is it possible for a degree measure to be negative?
Yes, a degree measure can be negative. The angle, being measured in the opposite direction, is shown by the value which is followed by a negative sign. Regardless of whether there are positive or negative signs, the angle's size will not change. The sign is influenced by the angle's rotational orientation. A positive angle is produced by rotating counterclockwise, whereas a negative angle is produced by rotating clockwise.
3. What is the significance of degree measure?
The degree is generally used to refer to angular measurements. The radian is the chosen unit of angle measurement for most mathematical applications, even though the degree may be more widely used and many people have a stronger practical knowledge of angles in terms of degrees.
