Question

A concave polygon has ____ interior angles more than $ {180^ \circ } $
A. No
B. 3 angles
C. One or more
D. Less than 5

Answer 1

Hint: A concave polygon must have at least four sides, must have more than 3 sides. A concave polygon is a polygon which is not convex. A convex polygon is a polygon which has no interior angle greater than $ {180^ \circ } $ and no angle will be pointing inwards. A star polygon is a concave polygon.

Complete step-by-step answer:
We are given to find the number of interior angles more than $ {180^ \circ } $ in a concave polygon.
A concave polygon will have at least 4 sides. Concave describes a shape that is curved inwards or pointed inwards. A polygon is said to be concave when there are dents in it.
For example, a star is a concave polygon. The common polygons such as Rectangle, square, triangle, parallelogram, rhombus, trapezium are convex polygons because no angles in these polygons is more than $ {180^ \circ } $ .

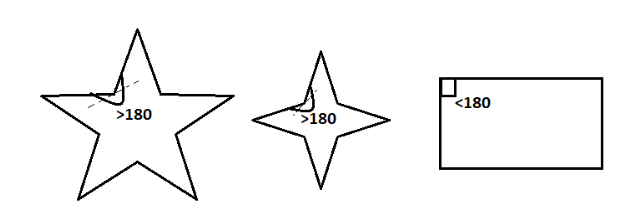
So a concave polygon is a polygon with at least one, one or more, interior angles greater than $ {180^ \circ } $
A concave polygon has one or more interior angles more than $ {180^ \circ } $

So, the correct answer is “Option C”.

Note: The sum of interior angles of a regular polygon with n sides can be given by the formula $ {180^ \circ }\left( {n - 2} \right) $ . Common polygons such as Rectangle, square, parallelogram, rhombus and trapezium with 4 sides have no angles greater than $ {180^ \circ } $ because all the interior angles of these angles add up to $ {180^ \circ }\left( {4 - 2} \right) = {180^ \circ } \times 2 = {360^ \circ } $ and $ {360^ \circ } $ must be divided among all the 4 angles. So each angle can measure at most $ {90^ \circ } $ . That is why these polygons are said to be convex polygons.