Question

A cubic meter of copper weighing 9000 kg is rolled into a square bar 9 m long. An exact cube is cut off from the bar. How much does it weigh?
A. 333.3 kg
B. 320.5 kg
C. 349.1 kg
D. 312.9 kg

Answer 1

Hint: The volume of 9000 kg copper is one cubic meter. This is rolled into a square bar which is 9m long. The square bar will have width. When an exact cube is cut off from this bar, then the cube edge length will be the width of the bar. Find the volume of the cut-off cube. Use this volume to find the weight of the cube.

Complete step-by-step answer:
We are given that a cubic meter of copper weighing 9000 kg is rolled into a square bar 9 m long.

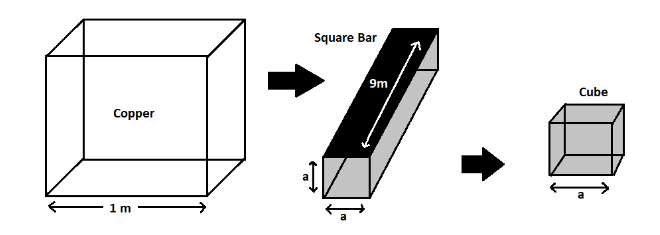
Let the width (side) of the square bar be ‘a’.
Volume of the copper is one cubic meter, $ 1{m^3} $
Volume of the square bar is $ 9 \times a \times a = 9{a^2}{m^3} $
The volume of the square bar must be equal to the volume of the copper.
 $
  Volum{e_{copper}} = Volum{e_{bar}} \\
   \Rightarrow 1{m^3} = 9{a^2}{m^3} \\
   \Rightarrow 1 = 9{a^2} \\
   \Rightarrow {a^2} = \dfrac{1}{9} \\
  \therefore a = \dfrac{1}{3}m \\
 $
The side of the square bar is $ \dfrac{1}{3}m $
Therefore, the edge of the cut-off cube from the square bar will also be $ \dfrac{1}{3}m $
Volume of the cube is $ \dfrac{1}{3} \times \dfrac{1}{3} \times \dfrac{1}{3} = \dfrac{1}{{27}}{m^3} $
 $ 1{m^3} $ weighs 9000 kg, then $ \dfrac{1}{{27}}{m^3} $ weighs $ \dfrac{1}{{27}} \times 9000 = 333.3kg $
The weight of the cube is 333.3 kg.

So, the correct answer is “Option A”.

Note: A square bar can also be considered as a cuboid, because all the edges of the square bar are not equal. There are 8 square edges and 4 rectangular edges in a square bar. A cuboid will have a length, a breadth and a height; since a square bar is also a cuboid its length and height are equal and breath is different.