Question

A cuboidal block of side 7 cm is surrounded by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Answer 1

Hint- Here, we will proceed by mounting the hemisphere on a cuboid of side 7 cm and the base of the largest hemisphere will be touching the edges of the top surface of the cuboid. Then, we will use the formulas which are Surface area of cuboid = $6 \times {\left( {{\text{Side of the cuboid}}} \right)^2}$, Curved surface area of hemisphere = $2\pi {\left( {\text{R}} \right)^2}$ and Area of base of the hemisphere = $\pi {\left( {\text{R}} \right)^2}$.

Complete step-by-step answer:

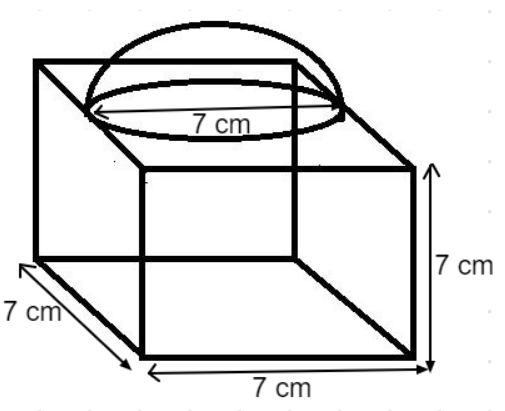
The hemisphere is mounted on a cubical block of side 7 cm as shown in the figure.
Given, Side of cuboid = 7 cm (i.e., all the dimensions in the cuboid will be equal to 7 cm)
From the figure, it can be easily seen that the greatest diameter that a hemisphere can have will be equal to the side of the cuboid.
So, greatest diameter of the hemisphere = Side of cuboid = 7 cm
As we know that Radius of the hemisphere = $\dfrac{{{\text{Diameter of the hemisphere}}}}{2}$
$ \Rightarrow $R = $\dfrac{7}{2} = 3.5{\text{ cm}}$
Since, the total surface area of a cuboid is given by
Surface area of cuboid = $6 \times {\left( {{\text{Side of the cuboid}}} \right)^2}{\text{ }} \to {\text{(1)}}$
Also, the curved surface area of any hemisphere of radius R is given by
Curved surface area of hemisphere = $2\pi {\left( {\text{R}} \right)^2}{\text{ }} \to {\text{(2)}}$
Also, the area of the base of any hemisphere having radius R is simply the area of a circular surface having radius R
i.e., Area of base of the hemisphere = $\pi {\left( {\text{R}} \right)^2}{\text{ }} \to {\text{(3)}}$
Total surface area of the solid will be equal to the sum of the surface area of the cuboid and the curved surface area of the hemisphere minus the area of base of the hemisphere.
i.e., Total surface area of the solid = Surface area of the cuboid + Curved surface area of the hemisphere - Area of base of the hemisphere
By using the formulas given by equations (1), (2) and (3), we get
Total surface area of the solid = $6 \times {\left( {\text{7}} \right)^2} + 2\pi {\left( {{\text{3}}{\text{.5}}} \right)^2} - \pi {\left( {{\text{3}}{\text{.5}}} \right)^2}$
By substituting $\pi = \dfrac{{22}}{7}$ in the above equation, we get
$ \Rightarrow $Total surface area of the solid = $6 \times {\left( {\text{7}} \right)^2} + 2\left( {\dfrac{{22}}{7}} \right){\left( {{\text{3}}{\text{.5}}} \right)^2} - \left( {\dfrac{{22}}{7}} \right){\left( {{\text{3}}{\text{.5}}} \right)^2} = 294 + 77 - 38.5 = 332.5{\text{ c}}{{\text{m}}^2}$
Therefore, the total surface area of the solid is 332.5 ${\text{c}}{{\text{m}}^2}$.
Note- The base of any hemisphere is always circular so the surface area of this circular base will be given by the formula i.e., Area of a circle = $\pi {\left( {\text{R}} \right)^2}$. In this particular problem, the base of the hemisphere is lying on the top surface of the cuboid, that's why that much portion will be subtracted when total surface area of the cuboid is taken in the evaluation of total surface area of the solid.