Question

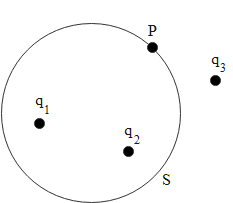
A Gaussian surface S encloses two charges \[{q_1} = q\] and ${q_2} = - q$. The field at P is:

$
  {\text{A}}{\text{. }}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} \\
  {\text{B}}{\text{. }}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \\
  {\text{C}}{\text{. }}\overrightarrow {{E_3}} \\
  {\text{D}}{\text{. }}\overrightarrow {{E_1}} + \overrightarrow {{E_2}} - \overrightarrow {{E_3}} \\
$

Answer 1

- Hint: The electric flux due to the charges enclosed in a hypothetical Gaussian surface is always due to the charges enclosed within the surface. There is no contribution to the flux due to charge outside the Gaussian surface.

Complete step-by-step solution -
Gauss law is used to calculate electric flux due to some charge in a region of space. It uses the concept of calculating the flux by enclosing the charge in a hypothetical surface called Gaussian surface. The Gauss law states that the electric flux due to some charges enclosed in a Gaussian surface is equal to $\dfrac{1}{{{ \in _0}}}$ times the total charge contained in inside the Gaussian surface. There is no contribution to the flux due to the charges outside the Gaussian surface.
We are given three charges ${q_1},{\text{ }}{q_2}$ and ${q_3}$. There is a hypothetical Gaussian surface which encloses charges ${q_1}$ and ${q_2}$ and it is given that
\[{q_1} = q\]
${q_2} = - q$
The third charge is outside the Gaussian sphere. There is point P on the surface of the Gaussian surface and we need to calculate the electric field at this point.
It can be calculated easily using the Gauss law in the following way:
Since the third charge is not contained inside the Gaussian surface so there is no contribution to electric flux on the Gaussian surface due to it.
Inside the Gaussian surface, we have charges ${q_1}$and ${q_2}$ only so the electric field at point P is equal to the vector sum of the electric field due to these two charges. It is given as
$\overrightarrow {{E_1}} + \overrightarrow {{E_2}} $
Hence, the correct answer is option A.

Note: 1. Vector addition of electric fields due to charges takes care of the negative and positive sign of the two charges due to which the total electric field $ \ne \overrightarrow {{E_1}} - \overrightarrow {{E_2}} $
2. The expression for Gauss law uses ${ \in _0}$ for vacuum but if the charges were present in a medium then permittivity of the medium is used.