Question

A hemispherical bowl of internal diameter 36 cm is filled with some liquid. This liquid is to be filled into cylinder shaped bottles each of radius 3 cm and height 6 cm. Find the number of bottles required to empty the bowl.

Answer 1

Hint: we will first find the total volume of the given hemispherical bowl using the formulae $ \dfrac{2}{3}\pi {{R}^{3}} $
Where R is the radius of the bowl and then we will find the volume of one cylinder shaped bottle using the formulae $ \pi {{r}^{2}}h $ where r is radius and h is height of the cylinder . To get the number of bottles required we will get the ratio of the two volumes. Volume is the keyword here as we need to find how much volume of liquid a hemispherical bowl needs and how many cylindrical bottles will be required to hold that much amount of liquid in them.

Complete step-by-step answer:
We know that,
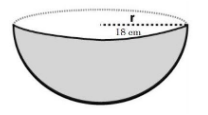
Diameter of the hemispherical bowl = 36 cm,
So, we can find the radius of the bowl as,
Radius(R) of the hemispherical bowl is = $ \dfrac{Diameter\,of\,Bowl}{2} $ = 18 cm

And also we are given that,
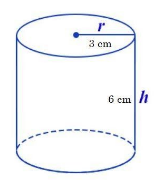
Radius(r) of the cylindrical shaped bottles is = 3 cm,
Height(h) of the cylindrical shaped bottles is = 6 cm,

Now, we will find the volume of hemisphere,
Volume of a hemisphere is given by the formula = $ \dfrac{2}{3}\pi {{R}^{3}} $
Now, by applying the above formula, we get
Volume of bowl = $ \dfrac{2}{3}\times \pi \times {{(18)}^{3}}\,c{{m}^{3}} $
And, now we will find the volume of the cylinder
Volume of a cylinder is given by = $ \pi {{r}^{2}}h $
Hence,
Volume of one cylindrical shaped bottle will be equal to = $ \pi \times {{(3)}^{2}}\times 6\,\,c{{m}^{3}} $
Now let us suppose the number of bottles required are $ x $ then volume of $ x $ cylindrical shaped bottles will be equal to the volume of hemispherical bowl,
First we’ll find the volume of $ x $ cylindrical shaped bottles,
Volume of $ x $ cylindrical shaped bottle = $ x\times \pi \times {{(3)}^{2}}\times 6\,\,c{{m}^{3}} $
Now, by equating the volume of hemisphere with the volume of $ x $ cylindrical shaped bottled, we get
 $ x $ $ \times $ $ \pi \times {{(3)}^{2}}\times 6 $ = $ \dfrac{2}{3}\times \pi \times {{(18)}^{3}}\, $
 $ \pi \times 54\times x=\dfrac{2\pi }{3}\times {{(18)}^{3}} $
After solving the above expression, we get
 $ x=72 $
Where $ x $ is the number of bottles required hence, 72 cylinder shaped bottles each of radius 3 cm and height 6 cm will be required to empty the hemispherical bowl of internal diameter 36 cm.

Note: In these types of questions you need to first try to find out what is the variable quantity here like in this question it was volume and try to go step by step and don’t skip any step in between it’ll increase your chances of solving it more easily and faster.
And also some students make a mistake while calculating the volume of hemispherical bowl, they just apply the formula for volume of sphere which is $ \dfrac{4}{3}\pi {{R}^{3}} $ but remember we need to find the volume for hemisphere hence it is half of the volume of sphere so, $ \dfrac{2}{3}\pi {{R}^{3}} $ should be applied.