
A metal sheet \[27\;cm\] long, \[8\;cm\] broad and \[1\;cm\] thick is melted into a cube so that volume is constant. The difference between surface areas of two solids is:
A. \[284\,c{m^2}\]
B. \[286\,c{m^2}\]
C. \[296\,c{m^2}\]
D. \[300\,c{m^2}\]
Answer
368.4k+ views
Hint:To solve the above problem we need to first find the metal sheet. As we know the length, height, and thickness we can find the total surface area of the cuboid formula. The sheet is then made into a cube. Given that the volume of both the metal sheet and a cube is constant. Therefore equating both the values we can find the edge length of the cube. After finding the edge length we can substitute this in the total surface area of the cube and then we can find the difference between the two.
Complete step by step answer:
Given that the length of the cuboid (metal sheet) is \[l\]=\[27\;cm\]
The height of the cuboid (metal sheet) is \[b\]=\[8\;cm\]
The thickness of the metal sheet \[h\]=\[1\;cm\]
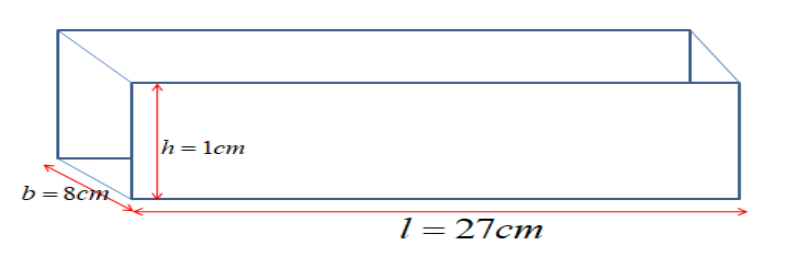
The total surface area of the cuboid (metal sheet) is given as= \[2\left( {lb{\text{ }} + {\text{ }}bh{\text{ }} + {\text{ }}hl} \right)\]
Therefore the surface area of the cuboid= \[2\left( {27 \times 8{\text{ }} + {\text{ 8}} \times 1{\text{ }} + {\text{ 27}} \times 1} \right)\]\[ = 502\;c{m^2}\]
The volume of the cuboid (metal sheet) is given as= \[lbh\]
The volume of the cube= \[{a^3}\]
We know that both the volume of the cuboid and the cube are equal.
Equating both the volumes,
\[{a^3} = lbh\]
\[ \Rightarrow {a^3} = 27 \times 8 \times 1\]
\[ \Rightarrow a = \sqrt[3]{{27 \times 8 \times 1}}\]
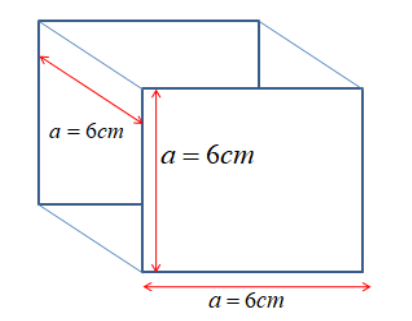
\[ \Rightarrow a = 6cm\]
Thus the total surface area (TSA) of the cube= \[6{a^2}\]
Substituting we get,
Hence the cube’s total surface area= \[6 \times {6^2} = 216c{m^2}\]
The difference between the total surface area of both metal sheet and cuboid is:
\[502\;c{m^2} - 216c{m^2} = 286c{m^2}\]
Therefore the correct option is B.
Note:Combinations of solids are solids that are made up of different types of shapes of solids that have one more basic shape. For example, the top which we use to play contains two shapes one is the hemisphere and the other is a cone. To find the total surface area of the solids we have to see first how many shapes that solid contains. Then we have to find the curved surface area of individual shapes and add them together to get the total surface area.
Complete step by step answer:
Given that the length of the cuboid (metal sheet) is \[l\]=\[27\;cm\]
The height of the cuboid (metal sheet) is \[b\]=\[8\;cm\]
The thickness of the metal sheet \[h\]=\[1\;cm\]
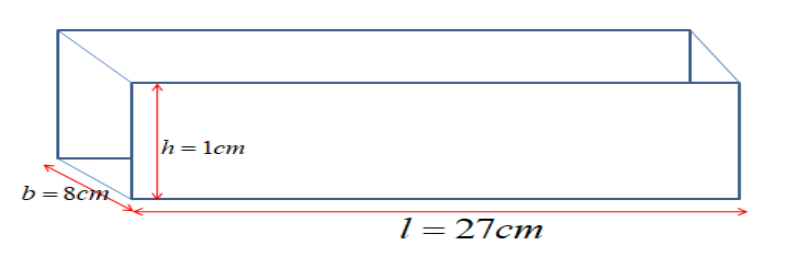
The total surface area of the cuboid (metal sheet) is given as= \[2\left( {lb{\text{ }} + {\text{ }}bh{\text{ }} + {\text{ }}hl} \right)\]
Therefore the surface area of the cuboid= \[2\left( {27 \times 8{\text{ }} + {\text{ 8}} \times 1{\text{ }} + {\text{ 27}} \times 1} \right)\]\[ = 502\;c{m^2}\]
The volume of the cuboid (metal sheet) is given as= \[lbh\]
The volume of the cube= \[{a^3}\]
We know that both the volume of the cuboid and the cube are equal.

Equating both the volumes,
\[{a^3} = lbh\]
\[ \Rightarrow {a^3} = 27 \times 8 \times 1\]
\[ \Rightarrow a = \sqrt[3]{{27 \times 8 \times 1}}\]
\[ \Rightarrow a = 6cm\]
Thus the total surface area (TSA) of the cube= \[6{a^2}\]
Substituting we get,
Hence the cube’s total surface area= \[6 \times {6^2} = 216c{m^2}\]
The difference between the total surface area of both metal sheet and cuboid is:
\[502\;c{m^2} - 216c{m^2} = 286c{m^2}\]
Therefore the correct option is B.
Note:Combinations of solids are solids that are made up of different types of shapes of solids that have one more basic shape. For example, the top which we use to play contains two shapes one is the hemisphere and the other is a cone. To find the total surface area of the solids we have to see first how many shapes that solid contains. Then we have to find the curved surface area of individual shapes and add them together to get the total surface area.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the color of ferrous sulphate crystals? How does this color change after heating? Name the products formed on strongly heating ferrous sulphate crystals. What type of chemical reaction occurs in this type of change.




