Question

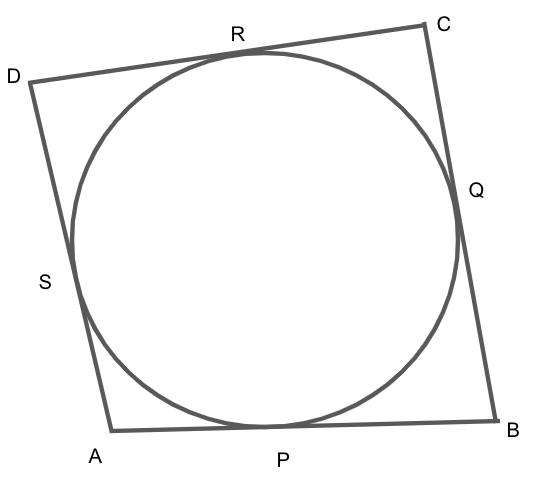
A quadrilateral ABCD is drawn to circumscribe a circle (see Figure). Prove that $$\text{AB}+\text{CD}=\text{AD}+\text{BC}$$.

Answer 1

Hint: First, we will use the tangents drawn from an exterior point to a circle are equal in length and then add the obtained equations. Then we will use the $$AP+BP=AB$$, $$BQ+CQ=BC$$, $$CR+DR=CD$$ and $$AS+DS=AD$$ to simplify this expression.

Complete step by step answer:

We are given that a quadrilateral ABCD is drawn to circumscribe a circle.
We know that tangents drawn from an exterior point to a circle are equal in length, so we have
$$\Rightarrow AP=AS\text{ ......eq.(1)}$$
$$\Rightarrow BP=BQ\text{ ......eq.(2)}$$
$$\Rightarrow CR=CQ\text{ ......eq.(3)}$$
$$\Rightarrow DR=DS\text{ ......eq.(4)}$$

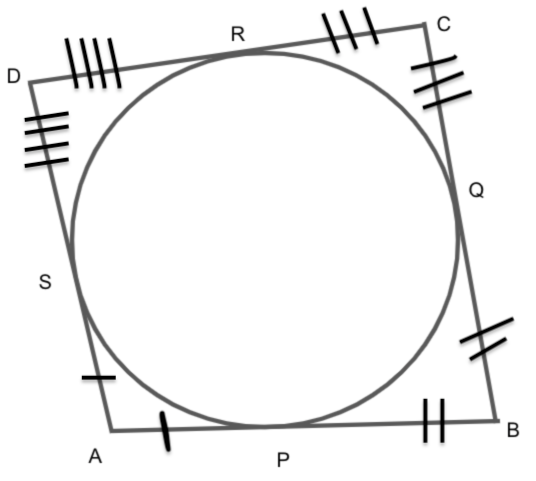
Adding the equations (1), (2), (3) and (4), we get
$$\Rightarrow AP+BP+CR+DR=AS+BQ+CQ+DS$$
Rewriting the above equation, we get
$$\Rightarrow \left(AP+BP\right)+\left(CR+DR\right)=\left(AS+DS\right)+\left(BQ+CQ\right)\text{ .......eq.(5)}$$
Since we also know that AB is a line segments and when any point P cuts this line segments, then $$AP+BP=AB$$.
From the same procedure, we get
$$BQ+CQ=BC$$
$$CR+DR=CD$$
$$AS+DS=AD$$
Using these sums from the given diagram in the equation (5), we get
$$\Rightarrow AB+CD=AD+BC$$
Hence, proved.

Note: In this question, we know that circumscribes a circle is to draw on the outside of just touching the corner points but never crossing. Here a quadrilateral is circumscribed around a circle. Students must crack the point of using that tangents drawn from an exterior point to a circle are equal in length. If we are able to crack this point, then the proof is very simple.