Question

A quadrilateral whose diagonals bisect each other are
(a) Parallelogram
(b) Square
(c) Triangle
(d) None of these

Answer 1

Hint: First all try to recollect the definition of quadrilaterals that is four sided polygons. Now select those quadrilaterals from options whose diagonals bisect each other.

Complete step-by-step answer:
In this question, we have to choose the quadrilateral whose diagonals bisect each other. Before proceeding with the question, let us first see what quadrilateral is and its basic types. A quadrilateral is a plane figure that has four sides or edges, so having four corners or vertices. Some examples of quadrilaterals are square, rectangle, parallelogram, etc. Now let us see some basic quadrilaterals and their properties.
1. Square: In square, all sides are equal, each interior angle measure $${90}^o$$. Its diagonals are equal and are perpendicular bisectors of each other.

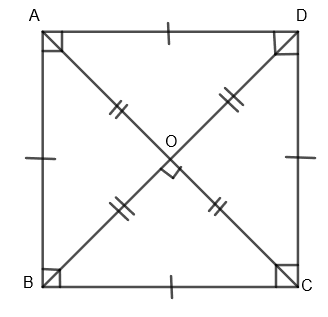
2. Rectangle: In a rectangle, opposite sides are equal in a rectangle, all angles in a rectangle are right angles and diagonals are equal and bisect each other.

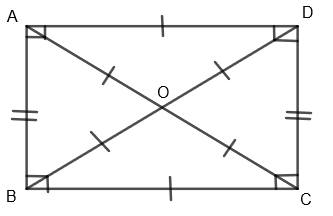
3. Rhombus: In rhombus, all sides are equal and diagonals are perpendicular bisectors of each other. Also, each diagonal is the angle bisector of both the opposite angles.

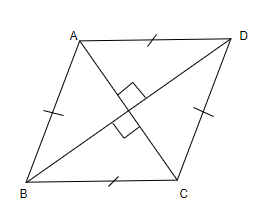
4. Parallelogram: In parallelogram, the opposite sides are parallel and equal to each other. Opposite angles are equal and the diagonals bisect each other.

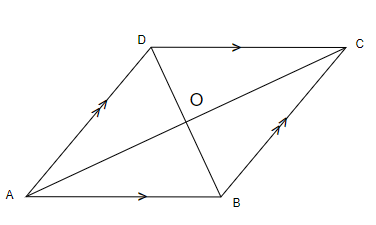
5. Trapezium: In trapezium, one pair of opposite sides is parallel. The diagonals intersect each other in the same ratio and two adjacent angles are supplementary.

Now let us consider our question. Here, we have to choose the quadrilateral whose diagonals bisect each other. As we have seen that in quadrilaterals such as square, rectangle, rhombus and parallelogram, the diagonals bisect each other. So the first two options are correct.
Now we know that the triangle is 3 sided polygon, so it is not quadrilateral and does not have diagonals so the third option is wrong.
Hence, options (a) and (b) are the correct answers

Note: Here, students must note that square is the most symmetrical quadrilateral among all quadrilaterals that’s why we can say that every square is rectangle, rhombus and parallelogram as well because square satisfies properties of all three. Similarly, we can say that every rhombus and every rectangle is a parallelogram but converse is not true for all these cases.