Question

a) What is the magnifying power of a microscope?
b) An object is placed at 20cm from a convex lens. If a 3 times magnified real image is formed by the lens then find the focal length of the lens.

Answer 1

Hint: a) Magnifying power means the ability of an instrument to magnify the image of an object observed by the observer. Here we will discuss the magnifying power of a microscope.
b) We have given the distance of the object from the lens, type of lens and the magnifying power of the lens. With the help of magnifying power formulas we can find the distance of an image from the lens. Once we find the distance of the image and object from the lens we can find the focal length by using lens formula.

Formula used:
\[\begin{align}
  & m=\dfrac{-v}{u} \\
 & \dfrac{1}{F}=\dfrac{1}{u}-\dfrac{1}{v} \\
\end{align}\]

Complete answer:
a) Magnifying power of a microscope is an ability of the instrument or microscope to produce an enlarged image of an object. Microscope has two formulas for magnifying power. One which gives linear magnification and another angular magnification.
Linear magnification is gives us the magnifying power of microscope when the eye is focused at near point as follows:
\[m=\left( 1+\dfrac{D}{f} \right)\]
Where f is the focal length of lens and D is the distance of image from the lens.
In case the eye is focused at infinity then the magnifying power or angular magnification is given as
\[m=\dfrac{D}{f}\]

b) According to the question we have to find the focal length of a convex lens, when distance of the object from the lens and its magnifying power is given.
The arrangement can be shown by a ray diagram as follows

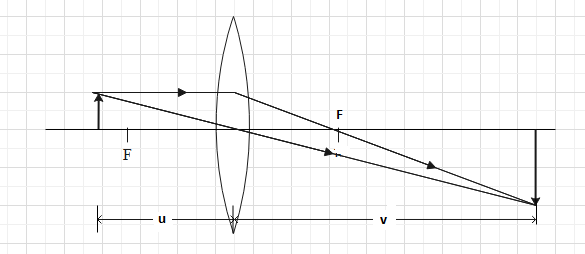
Magnifying power of a lens is the ratio of distance of image from the lens to the distance of object from the lens. Negative sign is used to show that the image is real. Magnifying power is given as
\[m=\dfrac{-v}{u}\], where m=3 and u=20cm
\[\begin{align}
  & v=-um \\
 & v=-(20\times 3) \\
 & v=-60cm \\
\end{align}\]
The focal length of convex lens is given as
\[\dfrac{1}{f}=\dfrac{1}{u}-\dfrac{1}{v}\]
Substituting values of u and v
\[\begin{align}
  & \dfrac{1}{F}=\left( \dfrac{1}{20} \right)-\left( -\dfrac{1}{60} \right) \\
 & \dfrac{1}{F}=\left( \dfrac{1}{20} \right)+\left( \dfrac{1}{60} \right) \\
 & \dfrac{1}{F}=\dfrac{80}{1200} \\
 & \dfrac{1}{F}=\dfrac{2}{30} \\
 & F=15cm \\
\end{align}\]

Hence the focal length of the given convex lens is 15cm.

Note:
Magnifying power of a lens or mirror is given by linear magnification as the eye is focused at a near object, angular magnification is for the instrument which is used to focus the eye at infinity like a telescope and microscope. The negative sign in the magnifying power of the lens shows that the image is real and inverted.
Convex lenses usually create a real and inverted image due to its converging property, but there is one case in which the convex lens creates an erect and virtual image.