Question

All squares are trapezium.
A). True
B). False

Answer 1

Hint: This question is a true or false type question. Given a statement that all the squares are trapezium. First, we need to state whether it is true or false or anything else and need to conclude with the explanation of the statement.

Complete step-by-step solution:
$\text{Square}$

$\text{TRAPEZIUM :-}$

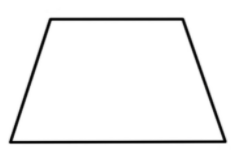
True, All the squares are trapezium because all squares have pairs of parallel sides. A trapezium is a quadrilateral in which the pair of opposite sides are parallel. Similarly squares also have two pairs of parallel sides. A square is a parallelogram with all sides equal and also all angles are equal. The other properties of the squares are the two diagonals of the squares are equal to each other and it divides the square into two equal and similar isosceles triangles whereas in trapezium the diagonals bisect each other. The length of the diagonals will be greater than the sides of the square. But not all the squares are trapezium. In square all angles are 90° but and so in trapezium and also diagonals are perpendicular bisectors but they are not so in trapezium. Thus every square is a trapezium but only some trapezium is a square. Thus the statement is true.
Final answer :
All squares are trapezium.
Option A). True

Note: Square is the plane geometrical figure. To state whether it is true or false in this question, we should know the concept of types of quadrilaterals and the properties of trapezium. We also conclude that all squares are trapezium but only some trapezium are squares.