
An air column in a tube 32 cm long, closed at one end, is in resonance with a tuning fork. The air column in another tube, open at both ends, of length 66 cm is in resonance with another tuning fork. When these two tuning forks are sounded together, they produce 8 beats per second. Then the frequencies of the two tuning forks are:
(Consider fundamental frequencies only)
A.250 Hz, 258 Hz
B.240 Hz, 248 Hz
C.264 Hz, 256 Hz
D.280 Hz, 272 Hz
Answer
583.5k+ views
Hint: As we all know that difference between the generated frequencies in the two given air columns gives the beats generated per second. Speed of sound depends upon the frequencies generated in closed and open air columns.
Complete step-by-step answer:
We can refer to the given figure below regarding the closed pipe and open pipe.
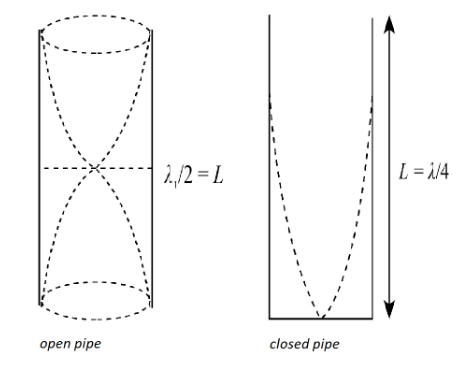
It is given to us in the question that,
The length of the closed air column is \[{L_1} = 32\;cm\]
The length of open air column is ${L_2} = 66\,cm$
The number of beats produced per second is $8\;$beats/sec.
We know that the velocity of the wave in two cases must be the same as the medium is the same. Velocity is given by the relation,
$V = n\lambda $
where V is the velocity, n is the frequency and $\lambda $ is the wavelength.
We know that the velocity in the given two cases of air column that is the open air column and the closed air column is the same as the medium is same. Therefore, the wavelength in close column is given by,
\[{\lambda _1} = 4{L_1}\]
We can substitute ${L_1} = 32\;cm$ to find the value of \[{\lambda _1}\].
\[\begin{array}{l}
{\lambda _1} = 4 \times 32\,cm\\
{\lambda _1} = 128\,cm
\end{array}\]
Here ${\lambda _1}$ is the wavelength and ${L_1}$ is the length of the air column
We know that for an open air column, the wavelength is given by.
${\lambda _2} = 2{L_2}$
We can substitute ${L_2} = 66\;cm$ to find the value of \[{\lambda _2}\].
$\begin{array}{l}
{\lambda _2} = 2 \times 66\;cm\\
{\lambda _2} = 132\;cm
\end{array}$
Here ${\lambda _2}$ is the wavelength and ${L_2}$ is the length of the air column
Since we know that the velocity is same, hence,
${V_1} = {V_2}$
Here ${V_1}$ and ${V_2}$ are the velocities of waves in closed air column and open air column respectively. Now we can substitute ${V_1} = {n_1}{\lambda _1}$ and ${V_2} = {n_2}{\lambda _2}$ in the above equation to equate the velocities. We can say that it becomes,
\[{n_1}{\lambda _1} = {n_2}{\lambda _2}\]
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\]
We can substitute \[{\lambda _1} = 128\,cm\] and \[{\lambda _2} = 132\;cm\] to find the value of \[\dfrac{{{n_1}}}{{{n_2}}}\].
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{132}}{{128}}\]
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{33}}{{32}}\] …… (I)
Also, it is given that ${n_1} - {n_2} = 8\,$ …… (II)
Solving equation (I) and (II), we get,
\[{n_1} = \dfrac{{33}}{{32}}{n_2}\]
We can substitute \[{n_1} = \dfrac{{33}}{{32}}{n_2}\] in equation (II) to find the value of \[{n_1}\], we get,
${n_1} = 264\,Hz$
We can substitute ${n_1} = 264\,Hz$ in equation (II) to find the value of \[{n_2}\], we get,
${n_2} = 256\;Hz$
We come to the point that the values of \[{n_1}\] and ${n_2}$ are $264\,Hz$ and $256\;Hz$ respectively.
Now we can say that the correct option is (C).
Note: Beat is like an interference pattern received as a periodic variation in sound among the sound waves of two different frequencies. By the help of tuning devices, we can easily recognize beats.
When two sound waves approach each other then the alternate destructive and constructive interference makes the sound wave either soft one time and loud one time in an alternate manner.
Complete step-by-step answer:
We can refer to the given figure below regarding the closed pipe and open pipe.

It is given to us in the question that,
The length of the closed air column is \[{L_1} = 32\;cm\]
The length of open air column is ${L_2} = 66\,cm$
The number of beats produced per second is $8\;$beats/sec.
We know that the velocity of the wave in two cases must be the same as the medium is the same. Velocity is given by the relation,
$V = n\lambda $
where V is the velocity, n is the frequency and $\lambda $ is the wavelength.
We know that the velocity in the given two cases of air column that is the open air column and the closed air column is the same as the medium is same. Therefore, the wavelength in close column is given by,
\[{\lambda _1} = 4{L_1}\]
We can substitute ${L_1} = 32\;cm$ to find the value of \[{\lambda _1}\].
\[\begin{array}{l}
{\lambda _1} = 4 \times 32\,cm\\
{\lambda _1} = 128\,cm
\end{array}\]
Here ${\lambda _1}$ is the wavelength and ${L_1}$ is the length of the air column
We know that for an open air column, the wavelength is given by.
${\lambda _2} = 2{L_2}$
We can substitute ${L_2} = 66\;cm$ to find the value of \[{\lambda _2}\].
$\begin{array}{l}
{\lambda _2} = 2 \times 66\;cm\\
{\lambda _2} = 132\;cm
\end{array}$
Here ${\lambda _2}$ is the wavelength and ${L_2}$ is the length of the air column
Since we know that the velocity is same, hence,
${V_1} = {V_2}$
Here ${V_1}$ and ${V_2}$ are the velocities of waves in closed air column and open air column respectively. Now we can substitute ${V_1} = {n_1}{\lambda _1}$ and ${V_2} = {n_2}{\lambda _2}$ in the above equation to equate the velocities. We can say that it becomes,
\[{n_1}{\lambda _1} = {n_2}{\lambda _2}\]
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\]
We can substitute \[{\lambda _1} = 128\,cm\] and \[{\lambda _2} = 132\;cm\] to find the value of \[\dfrac{{{n_1}}}{{{n_2}}}\].
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{132}}{{128}}\]
\[\dfrac{{{n_1}}}{{{n_2}}} = \dfrac{{33}}{{32}}\] …… (I)
Also, it is given that ${n_1} - {n_2} = 8\,$ …… (II)
Solving equation (I) and (II), we get,
\[{n_1} = \dfrac{{33}}{{32}}{n_2}\]
We can substitute \[{n_1} = \dfrac{{33}}{{32}}{n_2}\] in equation (II) to find the value of \[{n_1}\], we get,
${n_1} = 264\,Hz$
We can substitute ${n_1} = 264\,Hz$ in equation (II) to find the value of \[{n_2}\], we get,
${n_2} = 256\;Hz$
We come to the point that the values of \[{n_1}\] and ${n_2}$ are $264\,Hz$ and $256\;Hz$ respectively.
Now we can say that the correct option is (C).
Note: Beat is like an interference pattern received as a periodic variation in sound among the sound waves of two different frequencies. By the help of tuning devices, we can easily recognize beats.
When two sound waves approach each other then the alternate destructive and constructive interference makes the sound wave either soft one time and loud one time in an alternate manner.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who among the following opened first school for girls class 9 social science CBSE

What does the word meridian mean A New day B Midday class 9 social science CBSE

What is the full form of pH?

Write the 6 fundamental rights of India and explain in detail

Which places in India experience sunrise first and class 9 social science CBSE




