Question

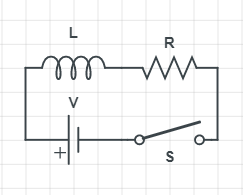
An inductor of inductance $L=\dfrac{\tau R}{2}$ and a resistor of resistance $R$ is connected to a battery of emf $V$ as shown in the figure. The potential difference across the resistance at a time $t=\tau ln2$ after the switch $S$ is closed is $k\;V$ . Find the value of $k$ ($\tau$ is constant)

Answer 1

Hint: Here, we have an LR series circuit, to find the potential difference across $R$ at some time $t$, we need to first calculate the total current in the circuit at any time, and then find the potential difference across the resistance $R$. then if we substitute the value of $t$ and equate the answer to $k\;V$, we can find the value of $k$.

Formula used:
$i=\dfrac{V}{R}\left(1-e^{-\dfrac{Rt}{L}}\right)$

Complete step by step answer:
Let $i$ be the current in the circuit, clearly it depends on the time, as there is an inductor in the circuit. Then the total current is expressed as $i=i_{r}+(i_{r}-i_{i})e^{-\dfrac{Rt}{L}}$.
Where, $i_{r}$ is the current flowing through the resistor$R$, $i_{l}$ is the current flowing through the inductor $L$ in time $t$.
Also $\tau$ is the time constant and it is given as $\tau=\dfrac{L}{R}$
Here, it is given that, inductance $L=\dfrac{\tau R}{2}$, resistance is$R$and an emf $V$is applied to the circuit, then from ohm’s law, we can write the $i_{r}=\dfrac{V}{R}$.
If $i_{i}=0$, then we get, $i=\dfrac{V}{R}-\dfrac{V}{R}e^{-\dfrac{Rt}{L}}=\dfrac{V}{R}\left(1-e^{-\dfrac{Rt}{L}}\right)$
$\implies V_{r}=V\left(1-e^{-\dfrac{Rt}{L}}\right)$, where $V_{r}$ is the voltage across the resistance $R$ and is given as,$V_{r}=iR$
From, $L=\dfrac{\tau R}{2}$
Rearranging, we get,$\dfrac{L}{R}=\dfrac{\tau}{2}$
Substituting, in the above, we get, $V_{r}=V\left(1-e^{-\dfrac{2t}{\tau}}\right)$
We need to find the potential difference across the resistance at a time $t=\tau ln2$ , hence substituting for in the above equation,
we get, $V_{r}=V\left(1-e^{-\dfrac{2\tau ln2}{\tau}}\right)$
$\implies V_{r}=V\left(1-e^{-2ln 2}\right)$
$\implies V_{r}=V\left(1-e^{-ln 4}\right)$
$\implies V_{r}=V\left(1+4\right)$
$\implies V_{r}=5V$
Given that $V_{r}=kV$
Then, we get $kV=5V$
$\implies k=5$
Hence the value of $k$ is $5$

Note:
$\tau$ is the value at which $\dfrac{V}{R}$ is the final steady state current flowing through the circuit, it is reached at $5\tau$. Also, after reaching this steady state current, the inductance of the coil reduces to zero. In a charging circuit, $5\tau$ is called the transient time of the circuit.