
What are forced vibrations and resonance? Show that only odd harmonics are present in an air column vibrating in a pipe closed at one end.
A stretched wire emits a fundamental note of frequency of 256Hz. Keeping the stretching force constant and reducing the length of wire by 10cm, the frequency becomes 320Hz. Calculate the original length of the wire.
Answer
502.8k+ views
Hint: The forced vibrations in an object or a system occurs, when the object or the system is forced to vibrate at a particular frequency. To achieve this, force is input into the system periodically. When the amplitude of the vibrations produced by the system is highest, that frequency is known as the resonant frequency of the system and the system vibrating at that frequency is known to be at resonance. To prove that only odd harmonics are present in an air column vibrating in a pipe closed at one end, we will make a diagram of the system and solve it.
The fundamental frequency of vibration is given by the relation:
Step by step solution:
Let’s start by defining the forced vibrations and resonance. The forced vibrations in an object or a system occurs, when the object or the system is forced to vibrate at a particular frequency. To achieve this, force is input into the system periodically. During this case, when the amplitude of the vibrations produced by the system is highest, that frequency is known as the resonant frequency of the system and the system vibrating at that frequency is known to be at resonance.
Now, let’s consider an organ pipe setup, with one end of the organ pipe closed. The length of the organ pipe is (L). Let’s consider (v) to be the speed of sound in air.
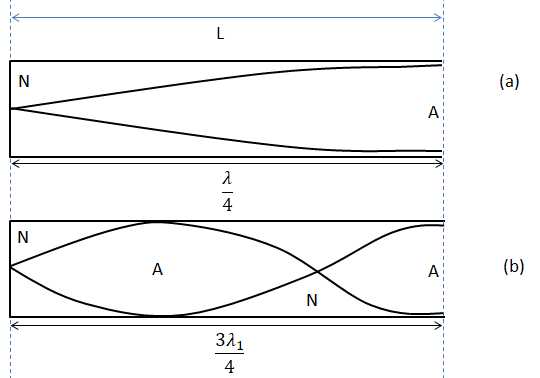
We know that when the sound waves travel down an air column in a cylindrical pipe which is closed at one end, then these waves are reflected back from the closed end. This reflected wave has a
The fundamental mode or first harmonic is given by diagram (a). The distance between nodes and the consecutive antinode is
Hence,
Let’s see the next higher mode of vibration known as the first overtone. This wave contains 2 nodes and 2 antinodes as shown in diagram (b). The wavelength of this wave is
Similarly, for second harmonic, the wavelength of this wave would be
The fundamental frequency of vibration is given by the relation:
Therefore,
Now,
Substituting in the value of (L) from the previous equation (1), we get;
That is;
Note: Every material has a resonant frequency at which it will produce highest amplitude oscillations. To understand, an example of resonance, you might have heard that people are never asked to march on a bridge because, a large number of people marching on a bridge may cause the bridge to resonate at its resonant frequency, which will cause all the particles of the bridge to oscillate at the highest amplitude damaging the bridge. However, when people are walking normally, it is more likely that people’s normal walking frequency don’t match with each other, but in the case of marching, all the people march at the same frequency.
The fundamental frequency of vibration is given by the relation:
Step by step solution:
Let’s start by defining the forced vibrations and resonance. The forced vibrations in an object or a system occurs, when the object or the system is forced to vibrate at a particular frequency. To achieve this, force is input into the system periodically. During this case, when the amplitude of the vibrations produced by the system is highest, that frequency is known as the resonant frequency of the system and the system vibrating at that frequency is known to be at resonance.
Now, let’s consider an organ pipe setup, with one end of the organ pipe closed. The length of the organ pipe is (L). Let’s consider (v) to be the speed of sound in air.

We know that when the sound waves travel down an air column in a cylindrical pipe which is closed at one end, then these waves are reflected back from the closed end. This reflected wave has a
The fundamental mode or first harmonic is given by diagram (a). The distance between nodes and the consecutive antinode is
Hence,
Let’s see the next higher mode of vibration known as the first overtone. This wave contains 2 nodes and 2 antinodes as shown in diagram (b). The wavelength of this wave is
Similarly, for second harmonic, the wavelength of this wave would be
The fundamental frequency of vibration is given by the relation:
Therefore,
Now,
Substituting in the value of (L) from the previous equation (1), we get;
That is;
Note: Every material has a resonant frequency at which it will produce highest amplitude oscillations. To understand, an example of resonance, you might have heard that people are never asked to march on a bridge because, a large number of people marching on a bridge may cause the bridge to resonate at its resonant frequency, which will cause all the particles of the bridge to oscillate at the highest amplitude damaging the bridge. However, when people are walking normally, it is more likely that people’s normal walking frequency don’t match with each other, but in the case of marching, all the people march at the same frequency.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




