
How do you calculate \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right)\]?
Answer
438.3k+ views
Hint: We use the concept that arc means inverse of the function. We are given the value of sine of an angle. Use the trigonometric identity \[{\sin ^2}x + {\cos ^2}x = 1\] to find the value of cosine of the same angle. Divide sine of the angle by cosine of the angle to calculate tangent of the angle. Use a quadrant diagram to write the value of angle for cosine.
* Arc sine of a function is defined as the inverse sine of the function. When \[\sin y = x\], then we can write \[\arcsin x = {\sin ^{ - 1}}x = y\].
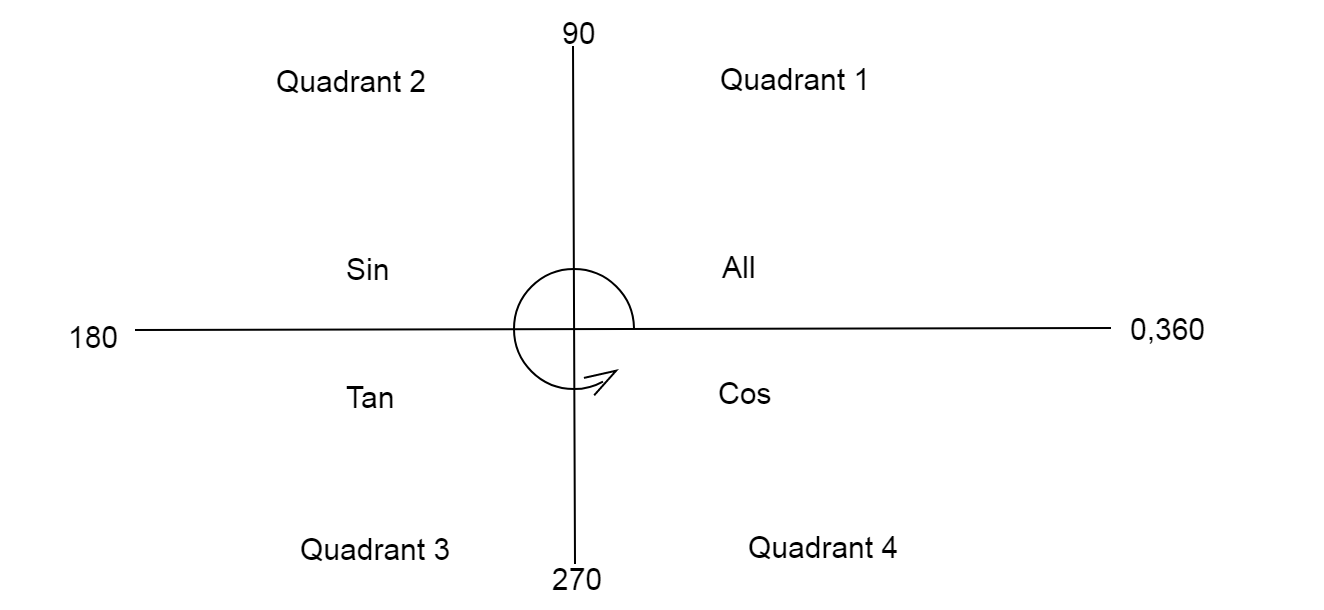
* We know the values of all trigonometric angles are positive in the first quadrant.
Values of only \[\sin \theta \] are positive in the second quadrant.
Values of only \[\tan \theta \] are positive in the third quadrant.
Values of only \[\cos \theta \] are positive in the fourth quadrant.
Complete step by step solution:
Let us assume the angle as ‘x’
We are given that \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right)\]
Since we know that \[\arcsin x = {\sin ^{ - 1}}x = y\]
Then we can write \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right) = {\sin ^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right) = y\]
\[ \Rightarrow {\sin ^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right) = y\]
Take sine on both sides of the equation
\[ \Rightarrow \sin \left[ {{{\sin }^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right)} \right] = \sin y\]
Cancel sine and sine inverse on left side of the equation
\[ \Rightarrow - \dfrac{{\sqrt 3 }}{2} = \sin y\] … (1)
We know that the value of \[\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2}\]
Also, we know sine is an odd function, so, \[\sin ( - x) = - \sin x\] and that sine function is negative in the third and fourth quadrant.
\[ \Rightarrow - \left( {\dfrac{{\sqrt 3 }}{2}} \right) = \sin y\]
\[ \Rightarrow - \left( {\sin \dfrac{\pi }{3}} \right) = \sin y\]
And we can write using the concept of odd function
\[ \Rightarrow \sin \left( { - \dfrac{\pi }{3}} \right) = \sin y\]
Take inverse sine function on both sides
\[ \Rightarrow {\sin ^{ - 1}}\left[ {\sin \left( { - \dfrac{\pi }{3}} \right)} \right] = {\sin ^{ - 1}}\left[ {\sin y} \right]\]
Cancel inverse function by the function
\[ \Rightarrow y = - \dfrac{\pi }{3}\]
\[\therefore \]The values of \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right)\] is \[ - \dfrac{\pi }{3}\]
Note: Many students make the mistake of calculating the angle inside sine as positive which is wrong, the value of sine is given negative so we will have to look at the quadrant diagram and figure out what is the sign of the angle. Keep in mind we can use table for trigonometric terms if we don’t remember the values at some common angles\[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\]
* Arc sine of a function is defined as the inverse sine of the function. When \[\sin y = x\], then we can write \[\arcsin x = {\sin ^{ - 1}}x = y\].
* We know the values of all trigonometric angles are positive in the first quadrant.
Values of only \[\sin \theta \] are positive in the second quadrant.
Values of only \[\tan \theta \] are positive in the third quadrant.
Values of only \[\cos \theta \] are positive in the fourth quadrant.

Complete step by step solution:
Let us assume the angle as ‘x’
We are given that \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right)\]
Since we know that \[\arcsin x = {\sin ^{ - 1}}x = y\]
Then we can write \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right) = {\sin ^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right) = y\]
\[ \Rightarrow {\sin ^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right) = y\]
Take sine on both sides of the equation
\[ \Rightarrow \sin \left[ {{{\sin }^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right)} \right] = \sin y\]
Cancel sine and sine inverse on left side of the equation
\[ \Rightarrow - \dfrac{{\sqrt 3 }}{2} = \sin y\] … (1)
We know that the value of \[\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2}\]
Also, we know sine is an odd function, so, \[\sin ( - x) = - \sin x\] and that sine function is negative in the third and fourth quadrant.
\[ \Rightarrow - \left( {\dfrac{{\sqrt 3 }}{2}} \right) = \sin y\]
\[ \Rightarrow - \left( {\sin \dfrac{\pi }{3}} \right) = \sin y\]
And we can write using the concept of odd function
\[ \Rightarrow \sin \left( { - \dfrac{\pi }{3}} \right) = \sin y\]
Take inverse sine function on both sides
\[ \Rightarrow {\sin ^{ - 1}}\left[ {\sin \left( { - \dfrac{\pi }{3}} \right)} \right] = {\sin ^{ - 1}}\left[ {\sin y} \right]\]
Cancel inverse function by the function
\[ \Rightarrow y = - \dfrac{\pi }{3}\]
\[\therefore \]The values of \[\arcsin \left( { - \dfrac{{\sqrt 3 }}{2}} \right)\] is \[ - \dfrac{\pi }{3}\]
Note: Many students make the mistake of calculating the angle inside sine as positive which is wrong, the value of sine is given negative so we will have to look at the quadrant diagram and figure out what is the sign of the angle. Keep in mind we can use table for trigonometric terms if we don’t remember the values at some common angles\[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\]
| ANGLEFUNCTION | \[{0^ \circ }\] | \[{30^ \circ }\] | \[{45^ \circ }\] | \[{60^ \circ }\] | \[{90^ \circ }\] |
| Sin | 0 | \[\dfrac{1}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{{\sqrt 3 }}{2}\] | 1 |
| Cos | 1 | \[\dfrac{{\sqrt 3 }}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{1}{2}\] | 0 |
| Tan | 0 | \[\dfrac{1}{{\sqrt 3 }}\] | 1 | \[\sqrt 3 \] | Not defined |
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




