Question

Why can’t you have zero to the power of zero?

Answer 1

Hint: In the above given problem, we are given an expression zero to the power of zero that can be written as \[{0^0}\] . We have to explain the reason behind the fact that why can not someone have zero to the power of zero. The main reason behind this problem is that zero to the power of zero gives us two different values with two different considerations.

Complete answer:
Given that, an expression of the form of zero to the power of zero.
That can be written as,
\[ \Rightarrow {0^0}\]
We have to explain the reason that why can not we take zero to the power of zero.
According to the general rule of exponents and powers, if we have an expression of the form \[{0^p}\] where \[p > 0\] , then we have the value
\[ \Rightarrow {0^p} = 0\]
For all the values of \[p > 0\] .
Also if we have \[ - p < 0\] then we have
\[ \Rightarrow {0^{ - p}} = \dfrac{1}{{{0^p}}}\]
Since, we have \[{0^p} = 0\] , we get
\[ \Rightarrow {0^{ - p}} = \dfrac{1}{0}\]
That is an undefined value.
But since, this rules are only accountable for \[p \ne 0\] .
Therefore, \[{0^p}\] for \[p = 0\] , i.e. \[{0^0}\] is not defined.
That is one value for the expression \[{0^0}\] , but if we consider a function \[y = {x^x}\] , then we need to check the value of this function at \[x = 0\] .
To find that, first we draw the graph for the function \[y = {x^x}\] .
That can be shown as the graph drawn below:

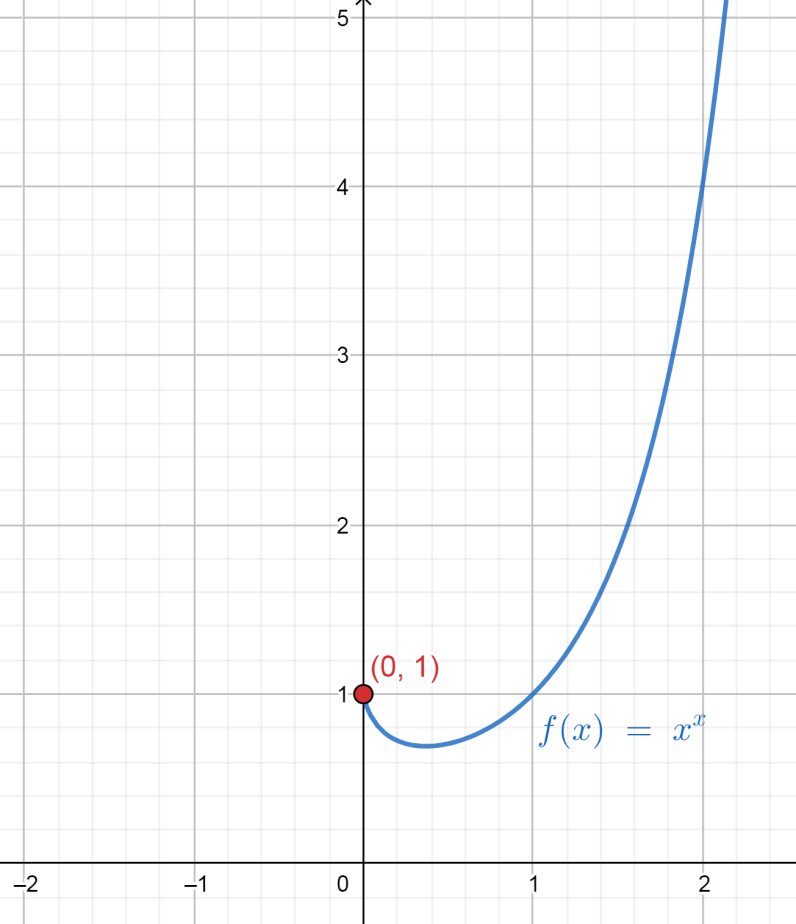
Here, since \[\left( {0,1} \right)\] lies on the graph of \[y = {x^x}\] ,
Therefore, we can see here that the graph shows the value for the function \[y = {x^x}\] at \[x = 0\] is equal to \[y = 1\] .
This is not because \[{0^0}\] is exactly equal to \[1\] every time, but because of the fact that in the neighbourhood of \[0\] the value of \[{x^x}\] is very close to \[1\] .
Therefore, there are two different values existing for the expression \[{0^0}\] , which are either \[1\] or not defined.
As a result, we can not find the exact value of \[{0^0}\] , hence we can not have zero to the power of zero.

Note: However, since now we know that we can not have zero to the power of zero as the value of the expression \[{0^0}\] is either \[1\] or not defined, but if we compare the two values precisely, then it is found that the value \[1\] is often more accurate and is taken at many places. For example, the limit of the function \[{n^n}\] when \[n\] is approaching \[0\] , is actually \[1\] i.e. \[\mathop {\lim }\limits_{n \to 0} {n^n} = 1\] .