Question

Count the number of faces, vertices, and edges of given polyhedra and verify Euler's formula. \[\]
1.

2.

3.

4.

Answer 1

Hint: We name each of the corners of the polyhedral which will be the vertices of the polyhedral. We name each of the polygonal faces and count the number of faces and edges. We recall Euler’s formula as $F+V=E+2$ where $F$ is the number of faces , $V$ is the number of vertices and $E$ is the number of edges.

Complete step-by-step solution:
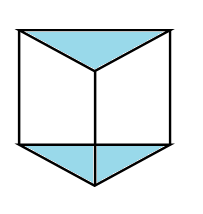
(1) We denote the vertices of one triangular face of the polyhedron at the bottom as A, B, C and other triangular face at the top as P,Q,R. So number of vertices is $V=3+3=6$. \[\]

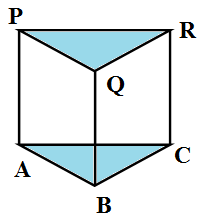
The edges are AB, BC, AC, PQ, QR, PR, AP, BQ and CR. So there are a total of 9 edges. So $E=9$. There are two triangular faces ABC and PQR. There are 3 quadrilateral faces ABQP, BCRQ and ACPR. So the number of faces is $F=2+3=5$. We have
\[\begin{align}
  & V+F=5+6=11 \\
 & E+2=9+2=11 \\
 & \therefore V+F=E+2 \\
\end{align}\]
Hence Euler’s formula is verified. \[\]

2.

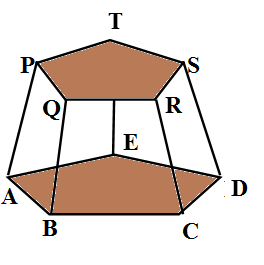
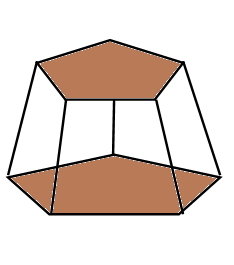
We denote the vertices of one pentagonal face at the bottom of the polyhedron as A, B, C,D,E and other pentagonal face at the top as P,Q,R,S,T. So number of vertices is $V=5+5=10$. \[\]
So there are 5 edges from each pentagon ABCDE and PQRST. The other edges are joining one vertex ABCDE to one vertex of PQRST which are AP, BQ, CR, DS, ET. So there are a total $5+5+5=15$ edges. So $E=15$. There are two pentagonal faces ABCDE and PQRST. There are 5 quadrilateral faces ABQP, BCRQ, SDSR, DETS and EAPT. So the number of faces is $F=2+5=7$. We have
\[\begin{align}
  & V+F=10+7=17 \\
 & E+2=15+2=17 \\
 & \therefore V+F=E+2 \\
\end{align}\]
Hence Euler’s formula is verified. \[\]
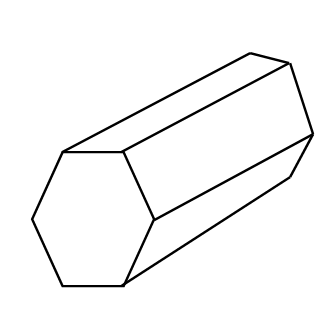
(3) We denote the vertices of one hexagonal face at the front of the polyhedron as A, B, C,D,E,F and other pentagonal faces at the back as P,Q,R,S,T,U. So number of vertices is $V=6+6=12$.\[\]

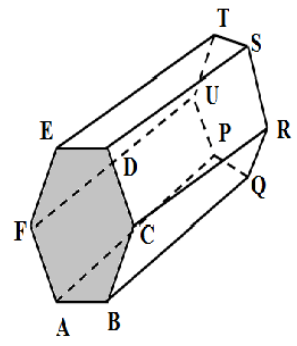
So there are 6 edges from each hexagon ABCDEF and hexagon PQRSTU. The other edges are joining one vertex ABCDEF to one vertex of PQRST which are AP, BQ, CR, DS, ET, FU. .So there are a total $6+6+6=18$ edges. So $E=18$. There are two hexagonal faces ABCDEF and PQRSTU. There are 6 quadrilateral faces ABQP, BCRQ, SDSR, DETS, EFUT and FAPU. So the number of faces is $F=2+6=8$. We have
\[\begin{align}
  & V+F=12+8=20 \\
 & E+2=18+2=20 \\
 & \therefore V+F=E+2 \\
\end{align}\]
Hence Euler’s formula is verified. \[\]
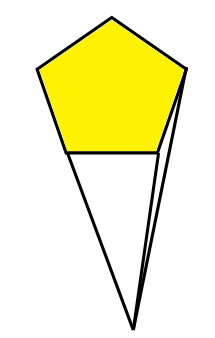
(4) We denote the vertices of the pentagon as A, B, C, D, E at the top and the corner at the bottom as P. So number of vertices is $V=5+1=6$\[\]

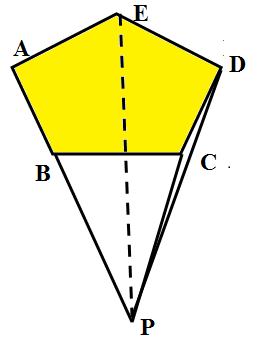
We see that there are 5 edges from each pentagon ABCDE as sides and other edges are joining the vertices of pentagon ABCDE to the corner P which are AP, BP, CP, DP and EP. So there are $E=5+5=10$ edges. There is one pentagonal face and other triangular faces are PAB, PBC, PCD, PDE and PEA. So there are $V=1+5=6$ faces. So we have
\[\begin{align}
  & V+F=6+6=12 \\
 & E+2=10+2=12 \\
 & \therefore V+F=E+2 \\
\end{align}\]
Hence Euler’s formula is verified. \[\]

Note: We note that the first, second and third polyhedron is prisms with triangular, pentagonal and hexagonal bases. The triangular and hexagonal prisms are also right prisms. The fourth polyhedron is a cone with a pentagonal base. We should be careful while finding the edges and faces because we need to visualize the back side of polyhedron dawn on lane paper.