
How do ‘d’ orbitals split in an octahedral crystal field?
Answer
573.3k+ views
Hint: All the valence orbitals of the metal cations are of the same energy(all the d orbitals have the same energy). We already know the crystal field theory called CFT. Crystal field theory states that the interaction between metal cations and ligands are electrostatic. The repulsive forces are the reason for the splitting of d orbitals.
Complete step by step answer:
We know that there are 5 lobes in the d orbital. They are ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$, ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$, ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$
-Electrons are filled subsequently in all these lobes.
-All the orbitals have the same energy which means that they are degenerate. But when a ligand is approaching the metal, the degeneracy is lost.
-The given below is ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ orbital. This means that it is in the z-axis and xy plane.

-The given below is ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$ orbital.

-Now, let us look at ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$.

-We already know that ligands are negatively charged and are coming to the metal cation through the axis.
-When a ligand is coming through the axis, the ligands overlap with ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$ and ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ orbitals since its lobes are lying on the axis. This will result in strong repulsion between the negative charge of electrons and the ligands in the axis.
-As we have already learnt in CFT, this repulsive force leads to splitting of the d orbital into higher energy ${{\text{e}}_{\text{g}}}$ and lower energy ${{\text{t}}_{{\text{2g}}}}$ levels.
-When ligands are approaching through the planes, it undergoes less repulsion and thus split into ${{\text{t}}_{{\text{2g}}}}$ levels. This happens when the ligand is approaching through xy, xz and yz planes. The orbital lobes which are in this plane are ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$ .
-So, In an octahedral Crystal field, d orbitals split into higher energy ${{\text{e}}_{\text{g}}}$ and lower energy ${{\text{t}}_{{\text{2g}}}}$
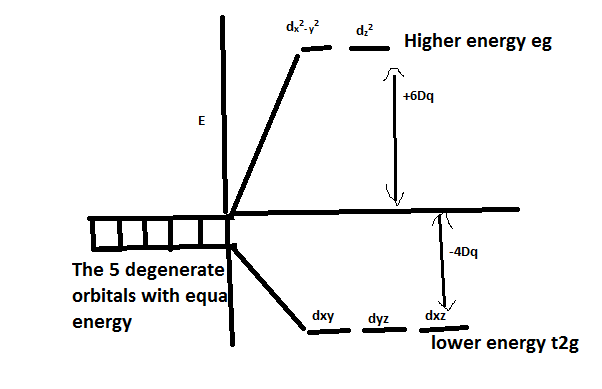
Note:The higher energy orbitals are those which undergo higher repulsion since its orbitals overlap with the approaching ligands. It is the opposite of the tetrahedral complex. In tetrahedral splitting, the higher energy is ${{\text{t}}_{{\text{2g}}}}$ and lower energy is ${{\text{e}}_{\text{g}}}$.
Complete step by step answer:
We know that there are 5 lobes in the d orbital. They are ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$, ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$, ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$
-Electrons are filled subsequently in all these lobes.
-All the orbitals have the same energy which means that they are degenerate. But when a ligand is approaching the metal, the degeneracy is lost.
-The given below is ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ orbital. This means that it is in the z-axis and xy plane.

-The given below is ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$ orbital.

It is in the x and y-axis.
-Now, let us look at ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$.

Similarly, ${{\text{d}}_{{\text{xz}}}}$ lies in the plane xz, ${{\text{d}}_{{\text{yz}}}}$ lies in the plane yz.
-We already know that ligands are negatively charged and are coming to the metal cation through the axis.
-When a ligand is coming through the axis, the ligands overlap with ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$ and ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ orbitals since its lobes are lying on the axis. This will result in strong repulsion between the negative charge of electrons and the ligands in the axis.
-As we have already learnt in CFT, this repulsive force leads to splitting of the d orbital into higher energy ${{\text{e}}_{\text{g}}}$ and lower energy ${{\text{t}}_{{\text{2g}}}}$ levels.
-When ligands are approaching through the planes, it undergoes less repulsion and thus split into ${{\text{t}}_{{\text{2g}}}}$ levels. This happens when the ligand is approaching through xy, xz and yz planes. The orbital lobes which are in this plane are ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{\text{yz}}}}$ .
-So, In an octahedral Crystal field, d orbitals split into higher energy ${{\text{e}}_{\text{g}}}$ and lower energy ${{\text{t}}_{{\text{2g}}}}$

Note:The higher energy orbitals are those which undergo higher repulsion since its orbitals overlap with the approaching ligands. It is the opposite of the tetrahedral complex. In tetrahedral splitting, the higher energy is ${{\text{t}}_{{\text{2g}}}}$ and lower energy is ${{\text{e}}_{\text{g}}}$.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers

State the principle of an ac generator and explain class 12 physics CBSE




