Question

Draw a circle, take three points one on the circle one in its interior and one in its exterior. Prepare a table showing rough figures and starting how many tangents can be drawn through each of three points.

Answer 1

Hint: We know that a line to a circle is called a tangent if it touches the circle only at one point and where the line touches the circle is known as point of contact. Using this fact we can find the number of tangents from different positions of points with respect to the circle.

Complete step-by-step answer:
A straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point. Also if the line is a tangent to circle, then it is perpendicular to the radius drawn to the point of tangency. Now according to the nature of the question, we have to mark three points with respect to the circle.
the 1st point will lie exactly on the circle and the 2nd point will lie inside the circle (interior) and the 3rd point will lie outside the circle. From all three different points we have to calculate the number of tangents that can be drawn to a given circle.

Case I.
When points lie on the surface or on circumference of the circle.
Let P be any point that lie on the circle with centre O

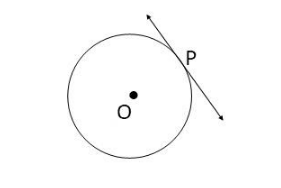
Now, draw a line through point P. We see that a line through P extending both sides never meets the circle again.
Hence, we see that line through P meet the circle only at one point. Therefore it will be a tangent line to circle.
Hence, from above we see that from a given point on the circle we can draw only one tangent to the circle.

Case II.

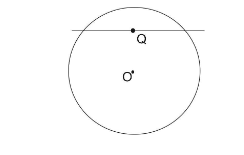
In this case we will take a point Q inside or interior of the circle of centre O. To find the number of tangents let draw a line through point Q. We see that a line which is drawn through point Q on extending both will meet the circle again at two different points.
Hence, this line can’t be a tangent to a given circle as by definition of tangent line, a line is said to be tangent if it touches the circle at only point.
Therefore, we see that when a point lies inside a circle there is no line drawn which touches the circle at one point.
Hence, from interior point the number of tangents that can be drawn to a given circle is equal to zero.

Case III:

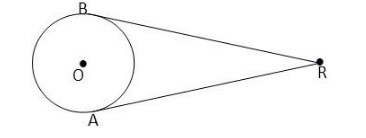
In this case we take a point R outside the circle.
To find the number of tangents that can be drawn from R. We first draw a line RB towards the circle in such a way that it meets the circle at a point B. Therefore, line RB is touching the circle only at one point. Hence, it will be a tangent to the circle by definition of tangent line.
But also, if we draw another line through R such that it meet same circle A as Point A is different from B and line through
R meets the circle only at one point. Therefore, line RA will also be a tangent line to the same circle.
Hence, from above we see that from an external point we can draw two tangents to a given circle.
Hence, from above we see that number of tangents that can be drawn from different position of point with respect to circle are given as:
Point in interior number of tangent = $0$
Point in Exterior number of tangents = $2$
Point on the circle number of tangent = $1$

Note: A line to a circle is said to be tangent if and only if it touches the circle only at one point even after extension along any side of the line. If a line cuts the circle at two points and passes through it will be named as secant line and a line which starts and ends on the circle called chord or diameter if it doesn't pass through centre or pass through centre respectively.