Question

Draw a circle with radius $2.5{\rm{ cm}}$. Draw a triangle of two angles $50^\circ $, $60^\circ $ with all its sides touching the circle.

Answer 1

Hint: This question is based on Geometry construction and we have to construct a triangle with given angles and all its sides touching a circle of given radius. In order to do this construction, we use a geometric property. According to this property “for an incircle of a triangle the two angles in front of each other have the same ratio as the other two angles for a triangle with a circle inside touching all its sides.”

Complete step-by-step answer:
Given:
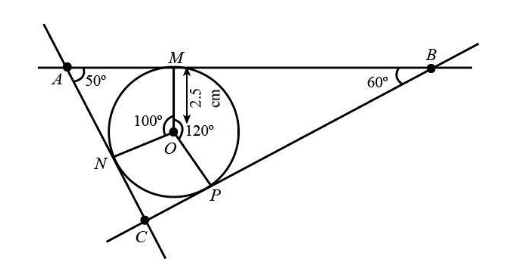
The radius of the circle $OM = {\rm{2}}{\rm{.5 cm}}$.
The two angles of the triangle $\angle A = 50^\circ $ and $\angle B = 60^\circ $.

The step by step construction is given below:
1) First take a radius of \[{\rm{2}}{\rm{.5 cm}}\] using the ruler scale and draw a circle taking O as the centre of the circle.
2) Now using the geometric property for the incircle of a triangle draw an angle $\angle MON$ of $100^\circ $ at the centre of the circle O.
3) Draw two perpendicular lines at the segments OM and ON starting from points M and N respectively in such a way that they intersect each other at a point A.
4) Now draw another angle $\angle MOP$ of $120^\circ $ at the line segment OM in the opposite direction to the earlier drawn angle in such a way that it intersects the circle at a point P.
5) Draw a perpendicular line on the line segment OP.
6) Now extend the perpendicular line of OP in such a way that it intersects the other two perpendiculars. Name the intersection points of the perpendiculars as B and C respectively.
Therefore, we have constructed a triangle $\Delta ABC$ having two angles of $50^\circ $ and $60^\circ $ with all its sides touching a circle with radius $2.5{\rm{ cm}}$.

Note: There are three quadrilaterals formed inside the $\Delta ABC$. These quadrilaterals are-
ONAM, OPCN, and OMBP.
We know that the sum of the interior angles of a quadrilateral is always $360^\circ $.