Question

Draw a graph of electric field vs distance for a solid sphere of radius $a$ containing charge $Q$ for $r \geqslant a$.

Answer 1

Hint: Use the relation between electric field and distance for a solid sphere. Electric field by a solid sphere is inversely proportional to the square of distance ($r \geqslant a$) from the center of the sphere.

Complete step by step answer:
We know that,
For a spherical charge of radius $a$,
$E = k\dfrac{Q}{{{r^2}}}$ outside the surface of the sphere.
On removing the constant of proportionality, we get,
$E \propto \dfrac{1}{{{r^2}}}$
The graph is given below:

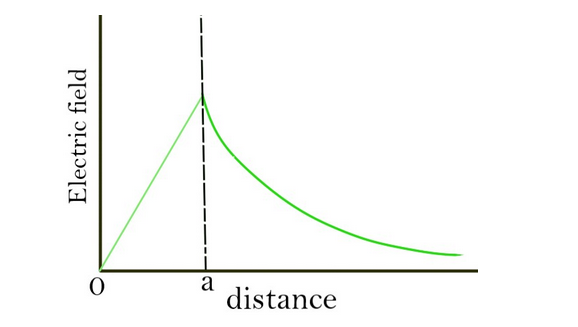
Additional information: An electric charge produces an electric field, which is a region of space around an electrically charged particle or object in which an electric charge would feel force. The electric field exists at all points in space and can be observed by bringing another charge into the electric field. However, the electric field can be approximated as zero for practical purposes if the charges are far enough from each other.
Electric fields are vector quantities and can be visualized as arrows going toward or away from charges. The lines are defined as pointing radially outwards, away from a positive charge, or radially inward, toward a negative charge.
The magnitude of the electric field is given by the formula $E = \dfrac{F}{Q}$, where $E$ is the strength of the electric field, $F$ is the electric force, and $Q$ is the test charge that is being used to “feel” the electric field.

Note: Electric field inside the solid sphere varies linearly with the distance. This can easily be derived with the help of Gauss’ law.
Let $\rho $be the charge density of the sphere.
Now,
We will take a loop at a distance R from the centre of the sphere as shown in the figure.

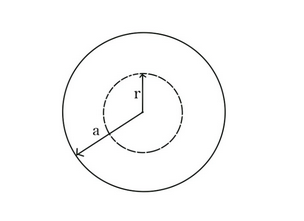
Gauss’ law states that
$\oint {E.ds = \dfrac{{{Q_{in}}}}{{{\varepsilon _0}}}} $
Where,
$E = $electric field
${Q_{in}} = $total charge inside the loop
We can find ${Q_{in}}$ by multiplying the charge density by the volume of the gaussian surface.
${Q_{in}} = \rho \times \dfrac{4}{3}\pi {r^3}$
Putting this in Gauss’ law,
$E\oint {ds = \dfrac{{\rho \times \dfrac{4}{3}\pi {r^3}}}{{{\varepsilon _0}}}} $
The integral of small area $ds$is equal to the surface area of the gaussian surface because $ds$is the small area on the gaussian surface.
Also,
Charge density is the charge per unit volume,
$\rho = \dfrac{Q}{{\dfrac{4}{3}\pi {a^3}}}$
Putting the value of $\rho $and $ds$, we get,
$E\left( {4\pi {r^2}} \right) = \dfrac{{\dfrac{{Q \times \dfrac{4}{3}\pi {r^3}}}{{\dfrac{4}{3}\pi {a^3}}}}}{{{\varepsilon _0}}}$
$E = \dfrac{{Qr}}{{4\pi {\varepsilon _0}{a^3}}}$.