Question

Draw a triangle of sides 5 cm and construct its incircle. Write the radius of the incircle.

Answer 1

Hint: In this particular question use the concept that if all the sides of a triangle are equal than it is an equilateral triangle and in an equilateral triangle all angles are equal to 60 degrees, and later on in the solution use that the tan is the ratio of perpendicular to base, so use these concepts to reach the solution of the question.

Complete step-by-step answer:
Given data:
A triangle of sides 5 cm.
As we all know that in a triangle there are 3 sides.
So it is given that the length of the sides is 5 cm.
Let us consider a triangle ABC, with AB = BC = CA = 5cm as shown in the below figure.

As we all know that if a triangle has all sides same then it is called an equilateral triangle.
And in an equilateral triangle all angles are equal.
In a triangle the sum of all angles is 180 degrees.
So let that measure of one angle be x degrees.
So, ${x^o} + {x^o} + {x^o} = {180^o}$
$ \Rightarrow 3{x^o} = {180^o}$
$ \Rightarrow {x^o} = {60^o}$
So in an equilateral triangle the measure of all the angles are equal to 60 degrees.
Now we have to construct its incircle
Steps of construction
$\left( i \right)$ Draw a triangle ABC with sides 5 cm as above.
$\left( {ii} \right)$ Now draw the bisector of any two angles, say angle B and angle C, let these bisectors intersect at point O, as shown in the below figure.

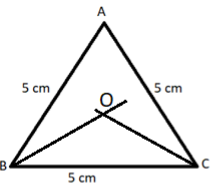
$\left( {iii} \right)$ Now draw a perpendicular from the intersection point O, of these two bisectors on line BC which cuts the line BC at point D, as shown in the below figure.

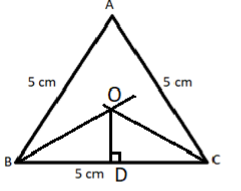
$\left( {iv} \right)$Now take a compass and in compass fill the length OD, with pointed end at O and pencil end at D and draw a circle which touches all the three sides as shown in the below figure.

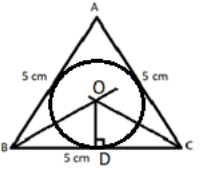
So this is the required incircle with center O.
Now we have to find out the radius of the incircle.
As shown in the above figure OD is the radius of the circle.
Now OB is a bisector of $\angle ABD$.
Therefore, $\angle OBD = \dfrac{{\angle ABD}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}$
And OD is perpendicular on BC, so BD = $\dfrac{{BC}}{2} = \dfrac{5}{2} = 2.5$ cm
Now in triangle OBD, tan x = (perpendicular/base).
Therefore, $\tan {30^o} = \dfrac{{OD}}{{BD}}$
$ \Rightarrow \tan {30^o} = \dfrac{{OD}}{{2.5}}$
$ \Rightarrow OD = 2.5\tan {30^o}$
$ \Rightarrow OD = 2.5 \times \dfrac{1}{{\sqrt 3 }} = 1.44 \simeq 1.5$ cm
So this is the required radius of the incircle.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that the bisector of any angle is divide the angle into two equal halves, and always recall the steps of construction which is stated above, these steps are the basis of the construction, without these steps we cannot draw the incircle.