Question

Draw two congruent circles of radii $3\text{ cm}$ , having their centers $10\text{ cm}$ apart. Draw a direct common tangent.

Answer 1

Hint: In this problem we need to draw two congruent circles of given radii. We know that the congruent circles are the circles which have similar properties like radius, area etc. First we will consider a point $A$ as the centre of the first circle. From this point draw a circle of radius $3\text{ cm}$ by using a compass. Now consider the center point of the first circle which is $A$ . We will mark a point which is $10\text{ cm}$ apart in any one of the directions and we can name it as $B$ . Now we will draw a second circle from the point $B$ with the help of a compass of radius $3\text{ cm}$. Now mark two points on the two circles from which we can draw a common tangent to both the circles.

Complete step-by-step solution:
Consider a point $A$ in the coordinate system as the centre of the first circle.

Constructing a circle of radius $3\text{ cm}$ by using the compass with point $A$ as centre, then we will get

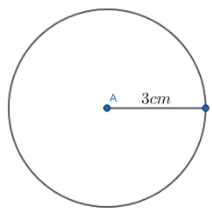
Now considering the point $A$ and marking another point $B$ which is $10\text{ cm}$ apart, then we will have

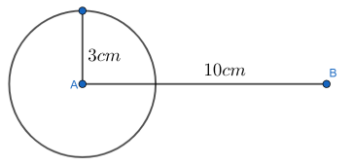
Now considering the point $B$ and constructing the circle of radius $3\text{ cm}$ by using compass and point $B$ as centre, then we will have

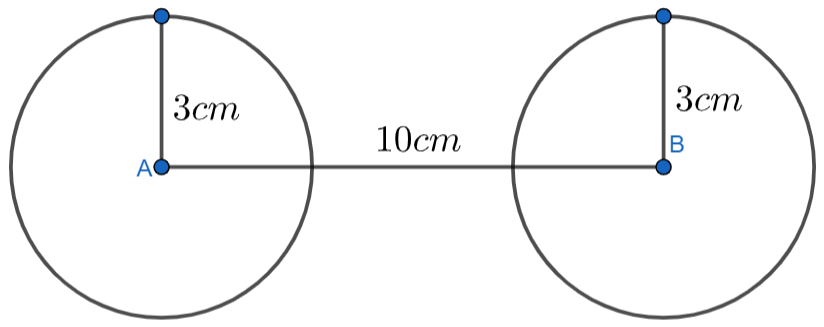
Considering the possible two points on the two circles to draw common tangent, then we will have

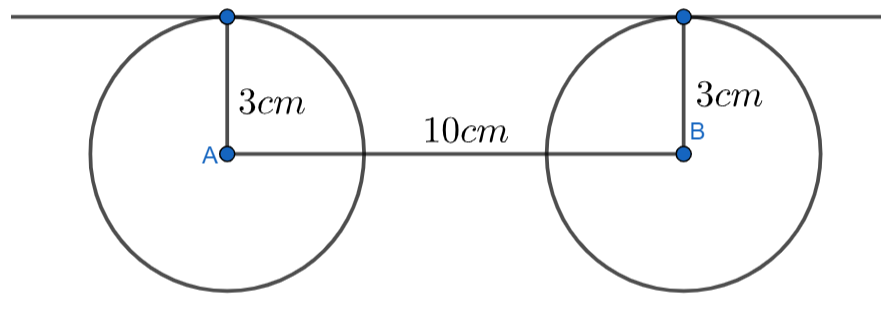
Note: In this problem we have asked to draw the common tangent to both the circles. We know that the tangent is a line which touches the circle at only one point. So the common tangent to both the circles is the line which touches the both circles at only one point.