Question

When an equilateral glass prism is in minimum deviation position,
i. the refracted ray is parallel to the base of the prism
ii. The angle of incidence is equal to the angle of emergence.
Choose the correct option.
A. only (i) is true
B. only (ii) is true
C. both (i) and (ii) are true
D. both (i) and (ii) are false

Answer 1

Hint: We know from refraction of light that light bends when it travels from one medium to another. The measure of bending is called the angle of deviation. It is also the difference in the angle between the extended incident angle and the refracted angle.

Complete step by step answer:
Let us consider an equilateral prism ABC such that the angle of the prism is $A$ and the refractive index of the prism is $\mu$. Let the incident light enter the prism at $P$ with an angle of incidence $i$. And let $r_{1}$ be the corresponding angle of refraction. Let the final angle of emergence be $e$. And let $r_{2}$ be the corresponding angle of refraction.

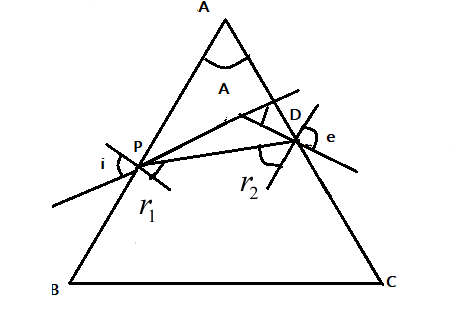
Let $D$ be the angle of deviation of the prism, then we know that the angle of deviation $D$ decreases with increase in $i$ to a particular angle after which further increase in the angle of incidence$i$ results in increase in angle of deviation$D$.
The $i-D$ graph is an upward parabola which gives the angle of emergence be $e$ for any given angle of incidence $i$.
The particular angle where the angle of deviation$D$ is minimum is called the minimum angle of deviation. This occurs when the angle of incidence $i$ is equal to the angle of emergence$e$. Also the refracted beam of light is parallel to the base of the prism.

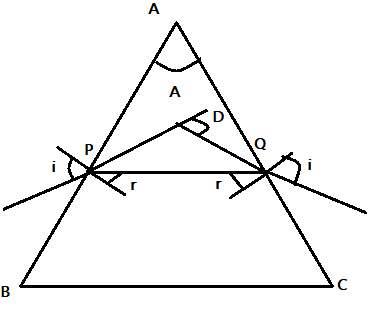
Hence the answer is C. both (i) and (ii) are true.

Note:
At the minimum angle of deviation the angle of refraction $r_{1}, r_{2}$ are equal. Also the angle of incidence is given as $i=\dfrac{A+D}{2}$ and the angle of refraction is given as $r=\dfrac{A}{2}$. Then the refractive index of the prism is given as $\mu=\dfrac{sin(=\dfrac{A+D}{2})}{sin(\dfrac{A}{2})}$.