
How many faces, edges and vertices does a pyramid have with n sided polygon as its base?
Answer
561k+ views
Hint: In this question, we have been asked the number of faces, edges and vertices a pyramid has.

To solve this question, we need basic idea about faces, edges and vertices of a three dimensional figure. Let's see the below labelled diagram of cuboid.
Observe that the above cuboid has 6 faces, 8 edges and 12 vertices.
Similarly, A pyramid is a 3 dimensional figure and the number of edges, faces and vertices depends on the sides of the base.
Moreover, we are not given any particular base of the pyramid. We have been asked the general formula with side ‘n’.
Complete step-by-step answer:
We have been asked the number of faces, edges and vertices of a pyramid whose base is unknown. We have to find a generalized formula in terms of ‘n’.
Before finding a generalized formula, let us look at certain pictures of a pyramid with different bases and find their faces, edges and vertices. Using them, we will derive the generalized formula.
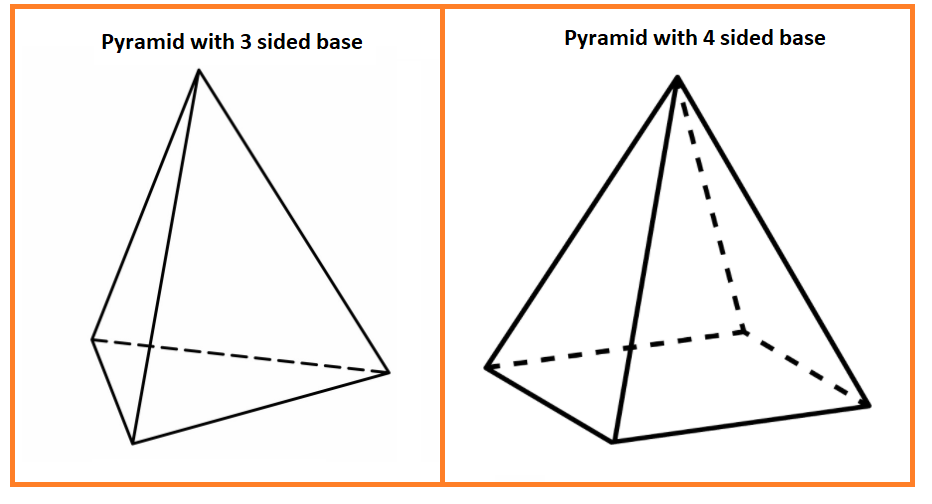
1) Faces:
(i) Pyramid with 3-sided base: This pyramid has 4 faces. One face which is the base and 3 faces connecting the base with the apex (top most vertex).
(ii) Pyramid with 4-sided base: This pyramid has 5 faces. One face as the base and other 4 faces connecting the base with the apex.
As we can notice, the total faces are one more than the number of sides of the base. Therefore, a pyramid with ‘n’ sided polygon as base will have $\left( {n + 1} \right)$ faces.
Complete step-by-step answer:
We have been asked the number of faces, edges and vertices of a pyramid whose base is unknown. We have to find a generalized formula in terms of ‘n’.
Before finding a generalized formula, let us look at certain pictures of a pyramid with different bases and find their faces, edges and vertices. Using them, we will derive the generalized formula.
1) Faces:
(i) Pyramid with 3-sided base: This pyramid has 4 faces. One face which is the base and 3 faces connecting the base with the apex (top most vertex).
(ii) Pyramid with 4-sided base: This pyramid has 5 faces. One face as the base and other 4 faces connecting the base with the apex.
As we can notice, the total faces are one more than the number of sides of the base. Therefore, a pyramid with ‘n’ sided polygon as base will have $\left( {n + 1} \right)$ faces.
2) Edges:
(i) Pyramid with 3-sided base: This pyramid has 6 edges – 3 edges making up the polygon as base and other 3 edges connecting the base to the apex.
(ii) Pyramid with 4-sided base: This pyramid has 8 edges – 4 edges making up the polygon as base and other 4 edges connecting the base to the apex.
If you will observe, the total edges are twice the number of sides of the base. Therefore, a pyramid with an ‘n’ sided polygon as base will have ($2n$) edges.
(i) Pyramid with 3-sided base: This pyramid has 6 edges – 3 edges making up the polygon as base and other 3 edges connecting the base to the apex.
(ii) Pyramid with 4-sided base: This pyramid has 8 edges – 4 edges making up the polygon as base and other 4 edges connecting the base to the apex.
If you will observe, the total edges are twice the number of sides of the base. Therefore, a pyramid with an ‘n’ sided polygon as base will have ($2n$) edges.
3) Vertices:
(i) Pyramid with 3-sided base: This pyramid has 4 vertices – 3 vertices of the base and 1 apex.
(ii) Pyramid with 4-sided base: This pyramid has 5 vertices – 4 vertices of the base and 1 apex.
On observation, we can tell that the total vertices are one more than the number of sides of the base.
Therefore, a pyramid with ‘n’ sided polygon as base will have $\left( {n + 1} \right)$ vertices.
Note: We can observe that a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with a polygonal base. A pyramid is usually assumed to be a regular square pyramid, like the physical pyramid structures. A triangle based pyramid is more often called a tetrahedron.
(i) Pyramid with 3-sided base: This pyramid has 4 vertices – 3 vertices of the base and 1 apex.
(ii) Pyramid with 4-sided base: This pyramid has 5 vertices – 4 vertices of the base and 1 apex.
On observation, we can tell that the total vertices are one more than the number of sides of the base.
Therefore, a pyramid with ‘n’ sided polygon as base will have $\left( {n + 1} \right)$ vertices.
Note: We can observe that a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with a polygonal base. A pyramid is usually assumed to be a regular square pyramid, like the physical pyramid structures. A triangle based pyramid is more often called a tetrahedron.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




