
Factorize the given polynomial \[{x^3} - 7x + 6\]
Answer
459.3k+ views
Hint: For this model first find out the one factor of the given polynomial by using trial method .Then after getting the one factor use the division method by using that factor . Use the formula \[dividend = divisor \times quotient + remainder\] for further simplification.
Complete step-by-step answer:
Given polynomial , \[{x^3} - 7x + 6\]
Let us take the given polynomial as \[p\left( x \right) = {x^3} - 7x + 6\]
Let us consider all the factors of the \[6\].
By using trial method
Let us substitute \[ - 1\] in the place of x. we get
\[\
p\left( { - 1} \right) = {\left( { - 1} \right)^3} - 7\left( { - 1} \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 2 \ne 0 \\
\ \]
Therefore, \[\left( {x + 1} \right)\] is not the factor of a given polynomial.
Again let us substitute \[1\] in the place of x . we get,
\[\
p\left( 1 \right) = {\left( 1 \right)^3}^{} - 7\left( 1 \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = 0 \\
\ \]
Therefore , \[\left( {x - 1} \right)\] is a factor of the given polynomial.
Now , let us find the quotient on dividing \[{x^3} - 7x + 6\] by \[\left( {x - 1} \right)\]
This can be solved by using method of long division
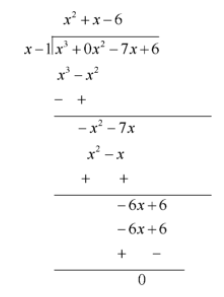
We know that ,
\[dividend = divisor \times quotient + remainder\]
Therefore , \[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right) + \left( 0 \right) \\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right).....\left( 1 \right) \\
\ \]
Let us consider \[q\left( x \right) = {x^2} + x - 6\]
Let us find the factors of the \[q\left( x \right) = {x^2} + x - 6\] by using factorization method
Comparing \[q\left( x \right) = {x^2} + x - 6\] with expression with \[a{x^2} + bx + c\]. We get \[a = 1,b = 1,c = - 6\]
Now multiply “a” term with “c” term and factor the product of (ac) such that the sum of factors equals to b .
The product of a, c is \[1\left( { - 6} \right) = - 6\]. Factor -6 as -2,3such that the sum of factors (-2)+3=1 which equals a coefficient of x that is b.
That is \[{x^2} + x - 6 = {x^2} + 3x - 2x - 6\]
In the next step , we are taking x as common in first two terms and -2 as common in next two terms
\[ = x\left( {x + 3} \right) - 2\left( {x + 3} \right)\]
Now taking \[\left( {x + 3} \right)\] from above equation
\[ = \left( {x + 3} \right)\left( {x - 2} \right)\]
Now substitute above factors in equation (1) , we get
\[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left[ {\left( {x + 3} \right) \times \left( {x - 2} \right)} \right] \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right) \\
\ \]
Thus , the factors of the given polynomial are \[\left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right)\]
Note: Factorization method is the process of factoring a polynomial into factors for which we use the several methods they are trial and error method, division method and the remainder theorem.
Complete step-by-step answer:
Given polynomial , \[{x^3} - 7x + 6\]
Let us take the given polynomial as \[p\left( x \right) = {x^3} - 7x + 6\]
Let us consider all the factors of the \[6\].
By using trial method
Let us substitute \[ - 1\] in the place of x. we get
\[\
p\left( { - 1} \right) = {\left( { - 1} \right)^3} - 7\left( { - 1} \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 2 \ne 0 \\
\ \]
Therefore, \[\left( {x + 1} \right)\] is not the factor of a given polynomial.
Again let us substitute \[1\] in the place of x . we get,
\[\
p\left( 1 \right) = {\left( 1 \right)^3}^{} - 7\left( 1 \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = 0 \\
\ \]
Therefore , \[\left( {x - 1} \right)\] is a factor of the given polynomial.
Now , let us find the quotient on dividing \[{x^3} - 7x + 6\] by \[\left( {x - 1} \right)\]
This can be solved by using method of long division
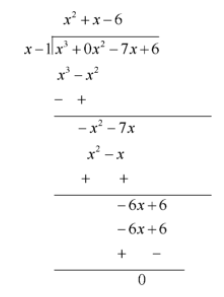
We know that ,
\[dividend = divisor \times quotient + remainder\]
Therefore , \[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right) + \left( 0 \right) \\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right).....\left( 1 \right) \\
\ \]
Let us consider \[q\left( x \right) = {x^2} + x - 6\]
Let us find the factors of the \[q\left( x \right) = {x^2} + x - 6\] by using factorization method
Comparing \[q\left( x \right) = {x^2} + x - 6\] with expression with \[a{x^2} + bx + c\]. We get \[a = 1,b = 1,c = - 6\]
Now multiply “a” term with “c” term and factor the product of (ac) such that the sum of factors equals to b .
The product of a, c is \[1\left( { - 6} \right) = - 6\]. Factor -6 as -2,3such that the sum of factors (-2)+3=1 which equals a coefficient of x that is b.
That is \[{x^2} + x - 6 = {x^2} + 3x - 2x - 6\]
In the next step , we are taking x as common in first two terms and -2 as common in next two terms
\[ = x\left( {x + 3} \right) - 2\left( {x + 3} \right)\]
Now taking \[\left( {x + 3} \right)\] from above equation
\[ = \left( {x + 3} \right)\left( {x - 2} \right)\]
Now substitute above factors in equation (1) , we get
\[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left[ {\left( {x + 3} \right) \times \left( {x - 2} \right)} \right] \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right) \\
\ \]
Thus , the factors of the given polynomial are \[\left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right)\]
Note: Factorization method is the process of factoring a polynomial into factors for which we use the several methods they are trial and error method, division method and the remainder theorem.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the color of ferrous sulphate crystals? How does this color change after heating? Name the products formed on strongly heating ferrous sulphate crystals. What type of chemical reaction occurs in this type of change.




