Question

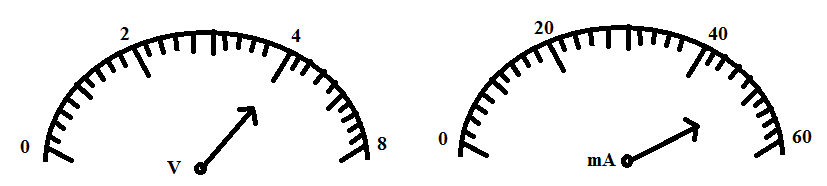
Figure shows analog voltmeter and ammeter. These meters are used to measure the potential difference across a resistor and the current through it. Assume that meters are ideal.

A. The percentage uncertainty in the calculation of resistance is 9 %
B. The percentage uncertainty in the calculation of power across the resistance is 8 %
C. The percentage uncertainty in the calculation of resistance is 1 %
D. The percentage uncertainty in the calculation of power across the resistance is 4 %

Answer 1

Hint: The formula of Ohm’s law should be used, as it relates the resistance, the current and the voltage (potential difference). Firstly, we will compute the value of the resistance using the values of the potential difference and the current displayed in the diagram. Finally, the change in these parameters, using the diagram should be noted down, and substituting the same in the formula, we can find the value of the percentage uncertainty.

Complete step by step answer:
From given, we have the data, that is, these values of the potential difference and the current are noted from the given diagram. So, we have,
The value of the potential difference is, V = 4 V
The value of the current is, I = 50 mA (as the pointer points in between the 40 mA and 60 mA)
Using the Ohm’s law, we will calculate the value of the resistance. So, we get,
\[\begin{align}
  & R=\dfrac{V}{I} \\
 & \Rightarrow R=\dfrac{4}{50\times {{10}^{-3}}} \\
\end{align}\]
Therefore, the value of the resistance is as follows.
\[\begin{align}
  & R=\dfrac{8}{0.1} \\
 & \Rightarrow R=80\Omega \\
\end{align}\]
Thus, the value of the resistance is\[80\Omega \].
Now, we will further continue the calculation by finding the value of the change in the resistance value.
The formula used to find the change in the values of resistance, the current and the potential difference is as follows.
\[\dfrac{\Delta R}{R}=\dfrac{\Delta V}{V}+\dfrac{\Delta I}{I}\]
The change in the value of the potential difference is calculated using the diagram. There are a total of 10 divisions and for this division value, the range is 0 to 2.
So, the change in the value of the potential difference is, \[\dfrac{2}{10}=0.2\].
The change in the value of the current is calculated using the diagram. There are a total of 10 divisions and for this division value, the range is 0 to 20.
So, the change in the value of the current is, \[\dfrac{20}{10}=2\].
Now substitute the above values in the equation. So, we get,
\[\begin{align}
  & \dfrac{\Delta R}{R}=\dfrac{0.2}{4}+\dfrac{2\times {{10}^{-3}}}{50\times {{10}^{-3}}} \\
 & \therefore \dfrac{\Delta R}{R}=\dfrac{0.1}{2}+\dfrac{1}{25} \\
\end{align}\]
Further continue the calculation.
\[\begin{align}
  & \dfrac{\Delta R}{R}=0.05+0.04 \\
 & \therefore \dfrac{\Delta R}{R}=0.09 \\
\end{align}\]
Now, represent the above change in the value in terms of per cent. Therefore, we get,
\[ \dfrac{\Delta R}{R} \% = 0.09\times 100 \]
\[ \therefore \dfrac{\Delta R}{R} \% = 9\% \]
As, the value of the percentage uncertainty in calculation of resistance is 9 %, thus, the option (A) is correct.

Note:
The change in the value of the current and the potential difference should be calculated using the diagram. Firstly compute the number of divisions present in between the values of the range. For example, in this question, we have calculated the change in the value of the current as, there are a total of 10 divisions and for this division value, the range is 0 to 20. So, the change in the value of the current is, \[\dfrac{20}{10}=2\].