Question

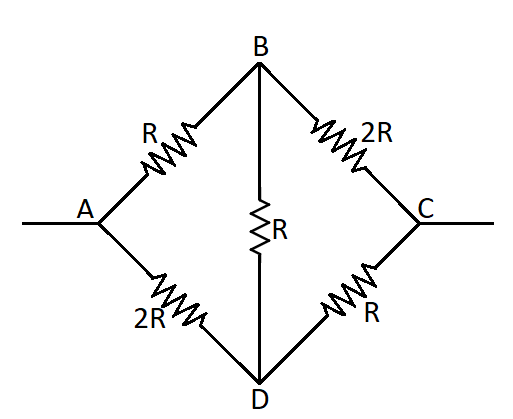
Find equivalent resistance between points A and B.

(A) $\dfrac{9}{4}R$
(B) $\dfrac{5}{3}R$
(C) $\dfrac{7}{5}R$
(D) $\dfrac{7}{4}R$

Answer 1

Hint
We first need to draw the equivalent circuit between the points A and B to simplify the diagram. Then by using the formula for calculating the equivalent resistance for parallel and series combination we need to find the resistance between the points A and B.

Formula Used: In this solution, we are going to use the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
And $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit.

Complete step by step answer
To find the equivalent resistance we need to first draw the simplified circuit between the points A and B. It is drawn as,

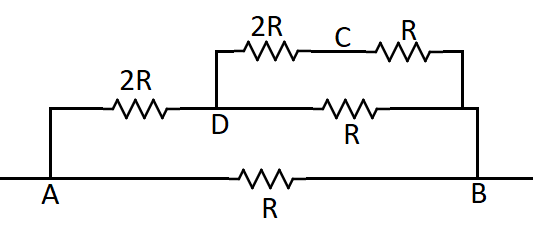
Now in the top wire between the points B and D we have 2 resistances which are in series with each other. So we can find the equivalent resistance by the formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
Now here we have, ${R_1} = 2R$ and ${R_2} = R$
So the equivalent will be,
${R_{eq1}} = 2R + R$
So we get the equivalent as,
${R_{eq1}} = 3R$
Now between the points B and D there are 2 resistances which are in parallel. So we get the equivalent by the formula,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Substituting the values of ${R_1} = {R_{eq1}} = 3R$ and ${R_2} = R$
So we get,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{1}{{3R}} + \dfrac{1}{R}$
Now taking the LCM as $3R$ we get,
$\dfrac{1}{{{R_{eq2}}}} = \dfrac{{1 + 3}}{{3R}}$
So taking the reciprocal we get,
${R_{eq2}} = \dfrac{{3R}}{4}$
Now in the top wire in between the points A and B we have 2 resistances which are in series.
So we use the formula, ${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where we substitute the values, ${R_1} = {R_{eq2}} = \dfrac{{3R}}{4}$ and ${R_2} = 2R$,
${R_{eq3}} = \dfrac{{3R}}{4} + 2R$
Now taking the LCM as 4,
${R_{eq3}} = \dfrac{{3R + 8R}}{4}$
Calculating we get,
${R_{eq3}} = \dfrac{{11R}}{4}$
In between A and B this resistance is in parallel to the resistance $R$. So we use the formula for parallel resistances where we substitute, ${R_1} = {R_{eq3}} = \dfrac{{11R}}{4}$ and ${R_2} = R$
$\dfrac{1}{{{R_{eq}}}} = \dfrac{4}{{11R}} + \dfrac{1}{R}$
On taking the LCM as $11R$ e get,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{{4 + 11}}{{11R}}$
On taking the reciprocal we get,
${R_{eq}} = \dfrac{{11R}}{{15}}$
So the equivalent resistance between the points A and B will be $\dfrac{{11R}}{{15}}$.
So, none of the options are correct.

Note
For the resistances which are in series, the current that is flowing through them will be the same. But for the resistances in parallel, the voltage across them will be equal and the current will depend on the value of the resistance.