Question

Find the ${14^{th}}$ and ${15^{th}}$ triangular numbers. And also find their sum.

Answer 1

Hint: A triangular number counts the number of dots arranged in an equilateral triangle. Or in simple words, nth triangular number is the number of dots in a triangular arrangement with n dots on a side, and is equal to the sum of n natural numbers from 1 to n.

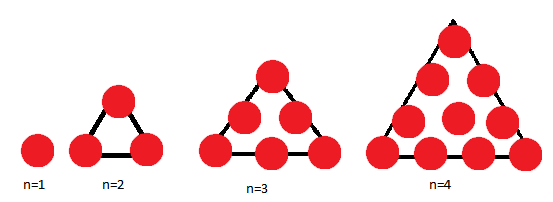
Complete step-by-step answer:
We can say that,\[{t_j} = \sum\limits_{i = 1}^j {i{\text{ }}} \] ,where ${t_j}$ is $j^{th}$ triangular number;
And also,${t_1} = 1{\text{ }}and{\text{ }}{t_j} = {t_{j - 1}} + j,{\text{for j}} \geqslant {\text{1}}$
Using the above definitions we can easily solve the question.
\[{t_j} = \sum\limits_{i = 1}^j {i{\text{ }}} = 1 + 2 + ... + j\]
Now, we know the sum of n numbers is given by${S_n} = \dfrac{{n(n + 1)}}{2},where{\text{ n}} \geqslant {\text{1}}$
So, \[{t_j} = \sum\limits_{i = 1}^j {i{\text{ }}} = 1 + 2 + ... + j = \dfrac{{j(j + 1)}}{2}\]
Now for calculating ${t_j}$ where j=14 put j=14 in above expression
So, ${t_{14}} = \sum\limits_{i = 0}^{14} i = \dfrac{{14(14 + 1)}}{2} = 7 \times 15 = 105$
For calculating ${t_{15}}$ ,
We know that $
  {t_{15}} = 1 + 2 + ... + 14 + 15 \\
   = {t_{14}} + 15 \\
 $
So, $
  {t_{15}} = {t_{14}} + 15 \\
   = 105 + 15 \\
   = 120 \\
 $
Now Sum of 14th and 15th triangular numbers = $
  {t_{15}} + {t_{14}} = 105 + 120 \\
   = 225 \\
$

225 is the required sum.

Note: In such questions you have to observe relations in the sequence. we can also find ${t_{15}}$ by \[{t_j} = \sum\limits_{i = 1}^j {i,{\text{where }}{t_j}{\text{ is jth triangular number; }}} \]but we used ${t_1} = 1{\text{ }}and{\text{ }}{t_j} = {t_{j - 1}} + j,{\text{for j}} \geqslant {\text{1}}$Because it is easy to calculate and will ease our calculations.