
How do you find the area of a regular octagon inscribed in a circle whose equation is given by ${(x - 2)^2} + {(y + 3)^3} = 25?$
Answer
446.7k+ views
Hint: According to the question we have to determine the area of a regular octagon inscribed in a circle whose equation is given by${(x - 2)^2} + {(y + 3)^3} = 25$. So, first of all we have to draw the image for the given situation as mentioned in the question that the regular octagon inscribed in a circle which is as below:
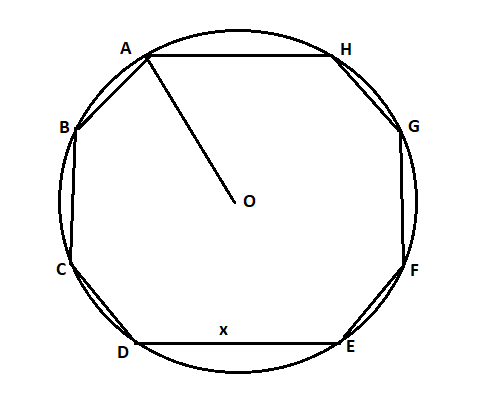
Where, ABCDEFGH is a regular octagon which is inscribed in a circle having centre O.
Now, first of all we have to determine the interior angle of the octagon which can be determined with the help of the formula to find the each interior angle of the octagon which is as explained below:
Formula used: $ \Rightarrow $Each interior angle $ = \dfrac{{{{360}^\circ}}}{n}$
Where, n is the total number of sides of the given polygon which is polygon for the given case.
Now, we have to determine the radius of the circle which can be determined with the help of the general form of the equation which is as mentioned below:
$ \Rightarrow {(x - {x_1})^2} + {(y - {y_1})^2} = {r^2}...........(B)$
Where, r is the radius of the given equation of the circle.
Now, we have to determine the area of the triangle AOB which is as formed in the octagon and there are total eight such triangles and to determine the area of the triangle with the help of the formula which is as mentioned below:
$ \Rightarrow $Area of the triangle(A)$ = \dfrac{1}{2}a \times h \times \sin \theta ..............(C)$
Where a, b are the sides of the triangle and $\sin \theta $ is the angle of the triangle we have already obtained.
Area of the octagon$ = 8A$
Where, a is the side of the octagon.
Complete step-by-step solution:
Step 1: First of all we have to draw the image for the given situation as mentioned in the question that the regular octagon inscribed in a circle which is as below:
Where, ABCDEFGH is a regular octagon which is inscribed in a circle having centre O.
Step 2: Now, we have to determine the interior angle of the octagon which can be determined with the help of the formula to find the each interior angle of the octagon which is as explained in the solution hint.
Hence, interior angle of the octagon,
$
= \dfrac{{{{360}^\circ}}}{8} \\
= {45^\circ}
$
Step 3: Now, we have to determine the radius of the circle which can be determined with the help of the general form of the equation which is as mentioned in the solution hint. Hence, on comparing the both of the equations.
$
\Rightarrow {r^2} = 25 \\
\Rightarrow r = \sqrt {25} \\
\Rightarrow r = 5
$
Step 4: Now, we have to determine the area of the triangle AOB which is as formed in the octagon and there are total eight such triangles and to determine the area of the triangle with the help of the formula (B) which is as mentioned in the solution hint. Hence,
$ \Rightarrow A = \dfrac{1}{2} \times 5 \times 5 \times \sin {45^\circ}$
Now, on substituting the value of $\sin {45^\circ} = \dfrac{1}{{\sqrt 2 }}$in the expression as obtained just above,
$
\Rightarrow A = \dfrac{1}{2} \times 5 \times 5 \times \dfrac{1}{{\sqrt 2 }} \\
\Rightarrow A = \dfrac{{25}}{{2\sqrt 2 }}
$
Step 5: Now, we have to determine the area of the octagon which can be determined with the help of the formula (C) which is as mentioned in the solution hint. Hence,
$
\Rightarrow {A'} = 8 \times \dfrac{{25}}{{2\sqrt 2 }} \\
\Rightarrow {A'} = 50\sqrt 2
$
Hence, with the help of the formulas (A), (B), and (C) we have determined the area of the octagon as inscribed in the circle which is $ = 50\sqrt 2 $.
Note: To determine the area of the triangle which is formed inside the octagon it is necessary that we have to determine the interior angle of the octagon with the help of the formula to determine the interior angle of the polygon.
We can determine the area of the octagon with the help of finding the area of the triangle as we know that there are eight triangles inside the octagon.

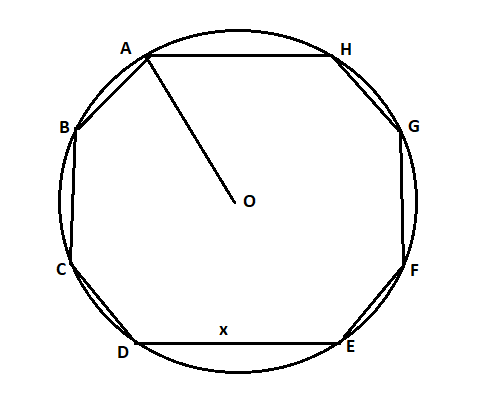
Where, ABCDEFGH is a regular octagon which is inscribed in a circle having centre O.
Now, first of all we have to determine the interior angle of the octagon which can be determined with the help of the formula to find the each interior angle of the octagon which is as explained below:
Formula used: $ \Rightarrow $Each interior angle $ = \dfrac{{{{360}^\circ}}}{n}$
Where, n is the total number of sides of the given polygon which is polygon for the given case.
Now, we have to determine the radius of the circle which can be determined with the help of the general form of the equation which is as mentioned below:
$ \Rightarrow {(x - {x_1})^2} + {(y - {y_1})^2} = {r^2}...........(B)$
Where, r is the radius of the given equation of the circle.
Now, we have to determine the area of the triangle AOB which is as formed in the octagon and there are total eight such triangles and to determine the area of the triangle with the help of the formula which is as mentioned below:
$ \Rightarrow $Area of the triangle(A)$ = \dfrac{1}{2}a \times h \times \sin \theta ..............(C)$
Where a, b are the sides of the triangle and $\sin \theta $ is the angle of the triangle we have already obtained.
Area of the octagon$ = 8A$
Where, a is the side of the octagon.
Complete step-by-step solution:
Step 1: First of all we have to draw the image for the given situation as mentioned in the question that the regular octagon inscribed in a circle which is as below:

Where, ABCDEFGH is a regular octagon which is inscribed in a circle having centre O.
Step 2: Now, we have to determine the interior angle of the octagon which can be determined with the help of the formula to find the each interior angle of the octagon which is as explained in the solution hint.
Hence, interior angle of the octagon,
$
= \dfrac{{{{360}^\circ}}}{8} \\
= {45^\circ}
$
Step 3: Now, we have to determine the radius of the circle which can be determined with the help of the general form of the equation which is as mentioned in the solution hint. Hence, on comparing the both of the equations.
$
\Rightarrow {r^2} = 25 \\
\Rightarrow r = \sqrt {25} \\
\Rightarrow r = 5
$
Step 4: Now, we have to determine the area of the triangle AOB which is as formed in the octagon and there are total eight such triangles and to determine the area of the triangle with the help of the formula (B) which is as mentioned in the solution hint. Hence,
$ \Rightarrow A = \dfrac{1}{2} \times 5 \times 5 \times \sin {45^\circ}$
Now, on substituting the value of $\sin {45^\circ} = \dfrac{1}{{\sqrt 2 }}$in the expression as obtained just above,
$
\Rightarrow A = \dfrac{1}{2} \times 5 \times 5 \times \dfrac{1}{{\sqrt 2 }} \\
\Rightarrow A = \dfrac{{25}}{{2\sqrt 2 }}
$
Step 5: Now, we have to determine the area of the octagon which can be determined with the help of the formula (C) which is as mentioned in the solution hint. Hence,
$
\Rightarrow {A'} = 8 \times \dfrac{{25}}{{2\sqrt 2 }} \\
\Rightarrow {A'} = 50\sqrt 2
$
Hence, with the help of the formulas (A), (B), and (C) we have determined the area of the octagon as inscribed in the circle which is $ = 50\sqrt 2 $.
Note: To determine the area of the triangle which is formed inside the octagon it is necessary that we have to determine the interior angle of the octagon with the help of the formula to determine the interior angle of the polygon.
We can determine the area of the octagon with the help of finding the area of the triangle as we know that there are eight triangles inside the octagon.
Recently Updated Pages
Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

What is the role of NGOs during disaster managemen class 9 social science CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Voters list is known as A Ticket B Nomination form class 9 social science CBSE




