
How do I find the area of a shaded region within a circle?
Answer
443.7k+ views
Hint: The given question describes the operation of finding the area of shaded position within a circle using mathematical formulae. Also, remind the general formula to find the area of a circle. Also, it involves the operation of addition/subtraction/multiplication/division. Consider the angle in degree, the distance in\[cm\].
Complete step-by-step solution:
In the given question, we would find how to calculate the area of a shaded region within the circle. For finding the method to find the area of the shaded region in a circle, we assume a diagram as given below,
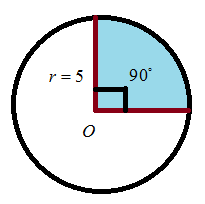
Here, the origin of the circle is mentioned as “\[o\]” and the radius of the circle is “\[r\]”. Also, the shaded region is marked in the above figure. So, we would find the area of the shaded region. Before that, we would remember the general formula for finding the area of the circle.
The area of circle A \[ = \pi {r^2}\]\[ \to \left( 1 \right)\]
Here \[\pi \] is constant, the value of \[\pi \]is\[3.14\]. And \[r\]is the radius of the circle. The general formula to find the area of the shaded region is given below
The area of the shaded region \[A = \pi \times {r^2} \times \dfrac{{angle}}{{360}}\]
Here the value of \[\pi \]is\[3.14\]and the value of \[r\]is\[5cm\]. The angle is 90 degrees which are given in the diagram. 360 degree is the total angle of a circle.
\[A = \pi \times {r^2} \times \dfrac{{angle}}{{360}}\]
\[A = \pi \times \left( {{5^2}} \right) \times \dfrac{{90}}{{360}}\]
\[
\\
A = \left( {3.14} \right) \times 25 \times \dfrac{{90}}{{360}} \\
A = \left( {3.14} \right) \times 25 \times \dfrac{1}{4} = \dfrac{{78.5}}{4} \\
A = 19.625c{m^2} \\
\]
Here the unit of area is\[c{m^2}\].
So, the area of the shaded region within the circle is\[19.625c{m^2}\].
Note: In the question, we would note the angle of the shaded region in degree. If the circle is shaded completely we can use the general formula (A\[ = \pi {r^2}\]) to find the area of the circle. Also, note that the total angle of the circle is\[360\]degrees. Every measurement should be positive.
Complete step-by-step solution:
In the given question, we would find how to calculate the area of a shaded region within the circle. For finding the method to find the area of the shaded region in a circle, we assume a diagram as given below,
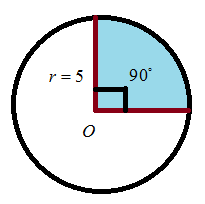
Here, the origin of the circle is mentioned as “\[o\]” and the radius of the circle is “\[r\]”. Also, the shaded region is marked in the above figure. So, we would find the area of the shaded region. Before that, we would remember the general formula for finding the area of the circle.
The area of circle A \[ = \pi {r^2}\]\[ \to \left( 1 \right)\]
Here \[\pi \] is constant, the value of \[\pi \]is\[3.14\]. And \[r\]is the radius of the circle. The general formula to find the area of the shaded region is given below
The area of the shaded region \[A = \pi \times {r^2} \times \dfrac{{angle}}{{360}}\]
Here the value of \[\pi \]is\[3.14\]and the value of \[r\]is\[5cm\]. The angle is 90 degrees which are given in the diagram. 360 degree is the total angle of a circle.
\[A = \pi \times {r^2} \times \dfrac{{angle}}{{360}}\]
\[A = \pi \times \left( {{5^2}} \right) \times \dfrac{{90}}{{360}}\]
\[
\\
A = \left( {3.14} \right) \times 25 \times \dfrac{{90}}{{360}} \\
A = \left( {3.14} \right) \times 25 \times \dfrac{1}{4} = \dfrac{{78.5}}{4} \\
A = 19.625c{m^2} \\
\]
Here the unit of area is\[c{m^2}\].
So, the area of the shaded region within the circle is\[19.625c{m^2}\].
Note: In the question, we would note the angle of the shaded region in degree. If the circle is shaded completely we can use the general formula (A\[ = \pi {r^2}\]) to find the area of the circle. Also, note that the total angle of the circle is\[360\]degrees. Every measurement should be positive.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the color of ferrous sulphate crystals? How does this color change after heating? Name the products formed on strongly heating ferrous sulphate crystals. What type of chemical reaction occurs in this type of change.




