Question

Find the area of an equilateral triangle with side 8 cm.

Answer 1

Hint: For solving this question firstly we will draw the figure of the given equilateral triangle and try to find the length of the height of the triangle by applying some basic concepts of trigonometry like $\sin \theta =\dfrac{\text{length of the perpendicular}}{\text{length of the hypotenuse}}$ . After that, we will find the value of the area by applying the formula $\dfrac{1}{2}\times \left( base \right)\times \left( height \right)$ correctly.

Complete step-by-step answer:
Given:
We have an equilateral triangle with side 8 cm, and we have to find the value of the area of the given equilateral triangle.
Now, let there be an equilateral triangle ABC with side 8 cm, and AD is the perpendicular drawn from the vertex A to the side BC and as it is an equilateral triangle AD will bisect the side BC. Moreover, as it is an equilateral triangle, the value of $\angle ABC=\angle BAC=\angle BCA={{60}^{0}}$. For more clarity look at the figure given below:

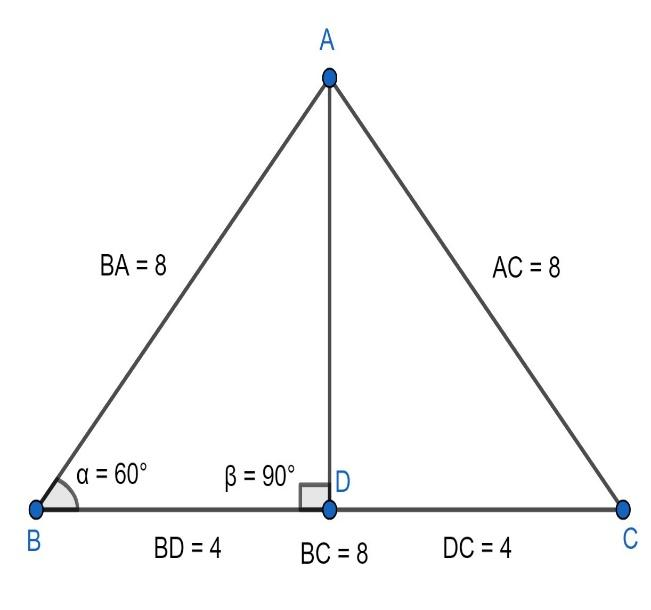
In the above figure, as AD bisects BC so, the length of BD will be equal to 4 cm.
Now, consider $\Delta ABD$ we have $AB=8,BD=4$ and $\angle ABD={{60}^{0}},\angle ADB={{90}^{0}}$. Then,
$\begin{align}
  & \sin \left( \angle ABD \right)=\dfrac{\left( \text{length of the perpendicular AD} \right)}{\left( \text{length of the hypotenuse BA} \right)} \\
 & \Rightarrow \sin {{60}^{0}}=\dfrac{AD}{BA} \\
\end{align}$
$\begin{align}
  & \Rightarrow AD=BA\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow AD=4\sqrt{3} \\
\end{align}$
Now, in the equilateral triangle ABC we have the length of the base BC equal to 8 cm and length of the height AD is equal to $4\sqrt{3}$ cm. Then,
$\begin{align}
  & Area=\dfrac{1}{2}\times \left( base \right)\times \left( height \right) \\
 & \Rightarrow Area=\dfrac{1}{2}\times 8\times 4\sqrt{3} \\
 & \Rightarrow Area=16\sqrt{3}\text{ c}{{\text{m}}^{2}} \\
\end{align}$
Now, from the above result, we conclude that the value of the area of the given equilateral triangle will be $16\sqrt{3}\text{ c}{{\text{m}}^{2}}$ .
Thus, the area of the given equilateral triangle will be 27.7128 sq. cm approximately.

Note: Here, the student should first understand the basic concepts of the equilateral triangle and then apply the basic concept of trigonometry. After that, find the height of the triangle and then calculate the value of the area of the triangle by the conventional formula. Moreover, for objective problems, we could use directly formula $\dfrac{\sqrt{3}}{4}{{a}^{2}}$ to find the area of an equilateral triangle of side $a$ units.