Question

Find the domain and range of the function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] .

Answer 1

Hint: To find the domain and range of the function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] , we will first consider the definition of signum functions which is given as
\[f\left( x \right) = \left\{ \begin{gathered}
  \begin{array}{*{20}{c}}
  1&{{\text{if}}}&{x > 0}
\end{array} \\
  \begin{array}{*{20}{c}}
  0&{{\text{if}}}&{x = 0}
\end{array} \\
  \begin{array}{*{20}{c}}
  { - 1}&{{\text{if}}}&{x < 0}
\end{array} \\
\end{gathered} \right....(i)\] . Next, we should consider the function \[\ln \left( {{x^2} - x + 2} \right)\] . We know that it is always positive for all real values of $x$ , that is, $x > 0$ . Now, let us see the function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] . From (i), we know that the value of this function is always 1 since \[\ln \left( {{x^2} - x + 2} \right)\] is positive. Now, draw the graph and find the domain and range. The domain of a function f(x) is the set of all values for which the function is defined or it is the set of all possible values of $x$ and range is the set of all values that f takes..

Complete step-by-step solution
We need to find the domain and range of the function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] . Let us first consider the range of signum functions.
We know that a signum function $f:R \to R$ is defined as
\[f\left( x \right) = \left\{ \begin{gathered}
  \begin{array}{*{20}{c}}
  1&{{\text{if}}}&{x > 0}
\end{array} \\
  \begin{array}{*{20}{c}}
  0&{{\text{if}}}&{x = 0}
\end{array} \\
  \begin{array}{*{20}{c}}
  { - 1}&{{\text{if}}}&{x < 0}
\end{array} \\
\end{gathered} \right....(i)\]
Now, we can consider the function
\[\ln \left( {{x^2} - x + 2} \right)\].
We know that all logarithmic functions are positive. Hence,
\[{x^2} - x + 2 > 0\]
Let us consider the entire function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] . From (i), we can see that for positive values of $x$ , that is, $x > 0$ , the signum function is 1. Hence, the value of
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right) = 1\]
The above equation means that for any values of x, the function
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\]
 will always be 1. Let us draw the graph of this.

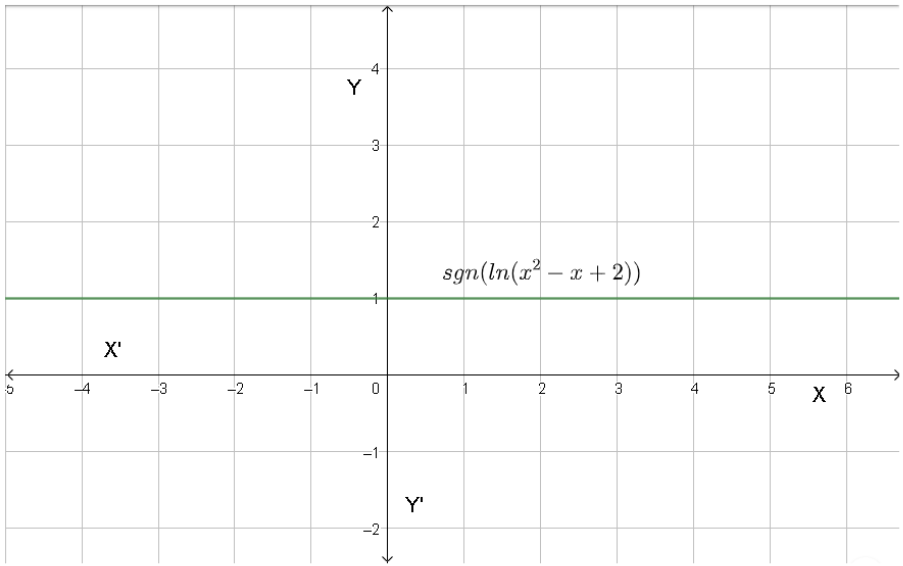
From the graph, we can find the domain and range. The domain of a function f(x) is the set of all values for which the function is defined or in other words, we can say that it is the all possible values of $x$ . We can see that, for all the real values of x, the function is 1. Hence, the domain is given as
$x \in R$
Now, we can find the range from the graph. Range of the function is the set of all values that f takes. We know that the function
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\]
 is always 1. Hence, the range of this function is given by
$f\left( x \right) = \operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right) = \left\{ 1 \right\}$

Note: There can be a chance of swapping the definitions for range and domain. You may define range as the set of all values for which the function is defined and domain as the set of all values that f takes. We can also find the value of \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] as follows.
We know that any real number can be expressed as the product of its absolute value and its sign function:
$x = \operatorname{sgn} \left( x \right).\left| x \right|$
For the function \[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right)\] , we can write the above form as
\[\ln \left( {{x^2} - x + 2} \right) = \operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right).\left| {\ln \left( {{x^2} - x + 2} \right)} \right|\]
We can write this as
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right) = \dfrac{{\ln \left( {{x^2} - x + 2} \right)}}{{\left| {\ln \left( {{x^2} - x + 2} \right)} \right|}}\]
We know that logarithmic functions are always positive. Hence, we get
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right) = \dfrac{{\ln \left( {{x^2} - x + 2} \right)}}{{\ln \left( {{x^2} - x + 2} \right)}}\]
Solving this, we will get
\[\operatorname{sgn} \left( {\ln \left( {{x^2} - x + 2} \right)} \right) = 1\]