Question

Find the height of the cone if the slant height h is 34cm and base diameter is 32cm.

Answer 1

Hint: First, we will consider the height of the cone as h1. Then we will find the radius of the cone by using the formula $ radius=\dfrac{diameter}{2} $ . Then we will use the formula $ \text{slant height=}\sqrt{heigh{{t}^{2}}+radiu{{s}^{2}}} $ . On putting the values and on solving, we will get the answer. Here the formula used will be $ {{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right) $ . Thus, we will get the height of the cone.

Complete step-by-step answer:
Here, we will first draw the diagram of cones with all dimensions given. So, diagram is as given below:

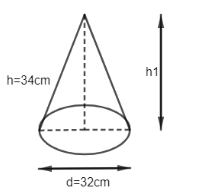
We have slant height h, diameter d as 32cm and we have assumed height of cone to be h1.
So, to find height of cone, the formula to be used is given as $ \text{slant height=}\sqrt{heigh{{t}^{2}}+radiu{{s}^{2}}} $ . So, we will first find the radius of the cone which can be given as $ radius=\dfrac{diameter}{2} $ .
On putting the value, we get as
Radius $ r=\dfrac{32}{2}=16cm $

Now, again substituting the value in the equation $ \text{slant height=}\sqrt{heigh{{t}^{2}}+radiu{{s}^{2}}} $ . So, we get as
 $ \text{h=}\sqrt{h{{1}^{2}}+{{r}^{2}}} $
 $ \text{34=}\sqrt{h{{1}^{2}}+{{\left( 16 \right)}^{2}}} $
Now, we will take squares on both sides, we will get as
 $ {{\left( \text{34} \right)}^{2}}\text{=}h{{1}^{2}}+{{\left( 16 \right)}^{2}} $
Now, we will make h1 as subject so, we get as
 $ h{{1}^{2}}\text{=}{{\left( \text{34} \right)}^{2}}-{{\left( 16 \right)}^{2}} $
Now, this above equation is in form $ {{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right) $ . So, here a is 34 and b is 16. So, on using this formula, we get as
 $ h{{1}^{2}}\text{=}\left( 34+16 \right)\left( 34-16 \right) $
On further solving, we get as
 $ h{{1}^{2}}\text{=}\left( 50 \right)\left( 18 \right) $
Now, taking square root on both sides, we get as
 $ h1\text{=}\sqrt{50\times 18}=\sqrt{25\times 2\times 9\times 2} $
Now, we can write this as
 $ h1\text{=5}\times \text{2}\times \text{3}=30cm $
Thus, the height of the cone is 30cm.

Note: Students should remember one formula which is used to find either radius, height or slant height which is given as $ \text{slant height=}\sqrt{heigh{{t}^{2}}+radiu{{s}^{2}}} $ . Also, mistakes happen in calculation so, be careful while solving the equation in order to avoid mistakes. Do not forget to convert diameter into radius otherwise the answer will be completely wrong.