Question

Find the length of longer diagonal of the parallelogram constructed on 5a+2b and a-3b, if it is given that $\left| a \right| = 2\sqrt 2 ,\left| b \right| = 3$ and the angle between a and b is $\dfrac{\pi }{4}$, is
A. 15
B. $\sqrt {113} $
C. $\sqrt {593} $
D. $\sqrt {369} $

Answer 1

Hint: First, we will add both the given vectors and find their resultant and then we calculate their magnitude by substituting the values in the formula. Afterwards, we compare both the answers and the greater one will be our required answer.

Complete step-by-step answer:

Given that, $\left| a \right| = 2\sqrt 2 ,\left| b \right| = 3$ and two sides of parallelogram are 5a+2b and a-3b. As you know, these are two given vectors of which we have to find the magnitude of resultants i.e. diagonals by using parallelogram law of vectors so that we can have the longest diagonal.
In parallelogram there are two cases to find the length of resultant vector:
1) Add both the vectors:

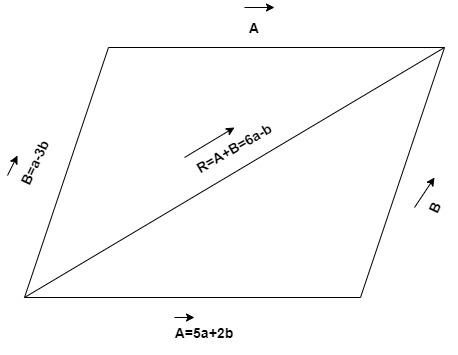
The resultant vector or one diagonal is 5a+2b+(a-3b) =6a-b=R
So, length of one diagonal
$ = \left| {6a - b} \right|$
Now, we calculate its magnitude by using formula $\sqrt {{a^2} + {b^2} - 2 \times \left| a \right| \times \left| b \right| \times \cos \theta } $, for vector subtraction, where there is negative sign in between them and where $\theta = \dfrac{\pi }{4}$
Substitute the value of both $\left| a \right|$ and $\left| b \right|$, we will get
$ = \sqrt {36{a^2} + {b^2} - 2 \times 6\left| a \right| \times \left| b \right| \times \cos 45^\circ } $, where $\cos \dfrac{\pi }{4} = \cos \dfrac{{180}}{4} = \cos 45^\circ $
Now, substitute the values in above equation
$ = \sqrt {36{{\left( {2\sqrt 2 } \right)}^2} + {3^2} - 2 \times 6\left( {2\sqrt 2 } \right) \times 3 \times \dfrac{1}{{\sqrt 2 }}} $, where $\cos 45^\circ = \dfrac{1}{{\sqrt 2 }}$
$
   = \sqrt {36 \times 8 + 9 - 72} \\
   = \sqrt {288 - 63} = \sqrt {225} = 15 \\
 $
2) Subtract one vector from other:

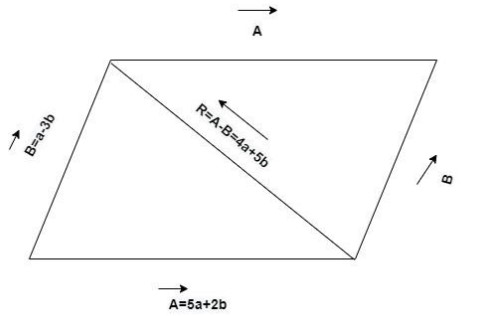
The resultant vector or other diagonal is 5a+2b-(a-3b) =4a+5b=R
Now, length of other diagonal is
$ = \left| {4a + 5b} \right|$
Similarly, we calculate its magnitude by using formula $\sqrt {{a^2} + {b^2} + 2 \times \left| a \right| \times \left| b \right| \times \cos \theta } $, for vector addition where there is a positive sign in between them and where $\theta = \dfrac{\pi }{4}$
Substitute the value of both $\left| a \right|$ and $\left| b \right|$ we will get,
$
   = \sqrt {16{a^2} + 25{b^2} + 2 \times 4\left| a \right| \times 5\left| b \right| \times \cos 45^\circ } \\
   = \sqrt {16{{\left( {2\sqrt 2 } \right)}^2} + 25{{\left( 3 \right)}^2} + 2 \times 4\left( {2\sqrt 2 } \right) \times 5\left( 3 \right) \times \dfrac{1}{{\sqrt 2 }}} \\
   = \sqrt {16 \times 8 + 25 \times 9 + 240} \\
   = \sqrt {128 + 225 + 240} = \sqrt {593} \simeq 24.35 \\
 $
Hence, 24.35 > 15 so the longer diagonal is 24.35 i.e. $\sqrt {593} $
Hence, the correct option is C.

Note: You should have thorough knowledge about the concept of Parallelogram law of vectors and how to find its magnitudes. As both the cases mentioned above follow the same concept and almost same formulas, so don’t get confused and calculate the result attentively to avoid mistakes. Only this method will help you to reach your result.