Question

Give analytical treatment of YDSE interference bands and hence obtain the expression for fringe width.

Answer 1

Hint: We will first consider a Young’s double slit experimental setup and then we will find the path difference. After we get the path difference, we will find out the expressions for the distances of bright and dark fringes from the central fringe. Then the fringe width can be calculated by measuring the distance of two consecutive bright and dark fringes and then subtracting them.

Complete step by step solution:
Let us consider a setup of the Young’s double slit experiment.

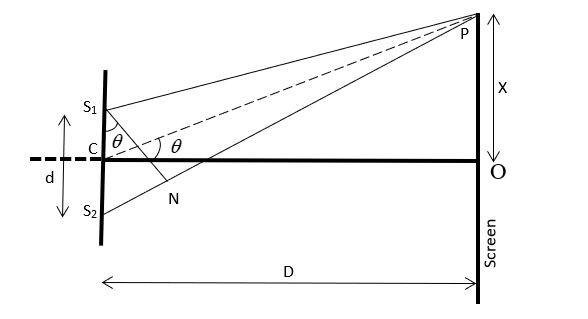
Here, ${S}_{1}$ and ${S}_{2}$ are the two parallel and closely spaced slits having equal widths and distance d between them. Two monochromatic coherent sources of light having wavelength $\lambda$ emerge through these two slits whose interference patterns can be seen on a screen placed D distance apart from the slits such that D >> d.
CN is the perpendicular bisector of ${S}_{1}{S}_{2}$ that intersects the screen at N.
Now, consider a point P on the screen at distance x from O, where the two light waves reach through paths ${S}_{1}P$ and ${S}_{2}P$ respectively. And ${S}_{1}N$ is a perpendicular on the path ${S}_{2}N$.
Now, from the figure, we can write that,
$({S}_{2}P)^2 =D^2 +(x+\dfrac{d}{2})^2$ ………. (i)
and $({S}_{1}P)^2=D^2 +(x-\dfrac{d}{2})^2$ ………. (ii)
Upon subtracting equation (i) from (ii), we will get
$({S}_{2}P)^2 – ({S}_{1}P)^2=D^2 +(x+\dfrac{d}{2})^2 -D^2 – (x-\dfrac{d}{2})^2$
On solving the equation, we will have
$\implies ({S}_{2}P +{S}_{1}P)({S}_{2}P-{S}_{1}P)=2xd$
$\implies {S}_{2}P-{S}_{1}P=\dfrac{2xd}{{S}_{2}P +{S}_{1}P}$
Practically, D is very much greater than x and d, such that ${S}_{2}P+{S}_{1}P\simeq 2D$
Therefore, path difference $({S}_{2}P-{S}_{1}P)=\dfrac{2xd}{2D}=\dfrac{xd}{D}$ ………. (iii)
The expression for fringe width (say X) can be found by finding the distance between two consecutive bright or dark fringes.
Now, if at point P, there is a bright fringe, then the path difference, $\dfrac{xd}{D}=n\lambda$, having n = 0, 1,2, 3….
And if at point P, there is a dark fringe, then the path difference, $\dfrac{xd}{D}=(2n-1)\dfrac{\lambda}{2}$, having n=1, 2, 3….
Now, let us assume that ${x}_{n}$ and ${x}_{n+1}$, be the distances of $n^{th}$ and $(n+1)^{th}$ bright fringe from the central maximum.
Therefore, ${x}_{n}=\dfrac{n\lambda D}{d}$……….. (iv)
and, ${x}_{n+1}=\dfrac{(n+1)\lambda D}{d}$ ………. (v)
Upon subtracting (v) from (iv), we get
Fringe width, $X=\dfrac{(n+1)\lambda D}{d}-\dfrac{n\lambda D}{d}=\dfrac{\lambda D}{d}(n+1-n) = \dfrac{\lambda D}{d}$
Hence, fringe width is given by $\dfrac{\lambda D}{d}$.

Note: The fringe width can be calculated by finding the distance between two consecutive dark or bright fringes. The distances between the two slits are very small and that is why they have been neglected in the derivation.