Question

How do you graph y = csc(x – 45)?

Answer 1

Hint: Here, this problem is based on cosecant function. It is the function which is derived from basic trigonometric function i.e. sine. This equation has to be graphically represented. The angle is given in degrees i.e. 45.

Complete step-by-step solution:
Now, let’s discuss its solution.
We all are aware of the basic functions of trigonometry. They are: sine, cosine and tangent. These are the building blocks of trigonometry. When we talk about derived functions, we say secant, cosecant and cotangent. Secant is derived from cosine, cosecant is derived from sine whereas cotangent is derived from tangent. Let’s see the relationship between basic functions and derived functions.
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$ or sin$\theta $ = $\dfrac{1}{\cos ec\theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$ or cos$\theta $ = $\dfrac{1}{sec\theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Here, $\theta $ is measure of an angle in degrees or radians.
Let’s see how we can find the value of sin$\theta $ and cosec$\theta $. First draw a right angled triangle with an angle $\theta $ at C.

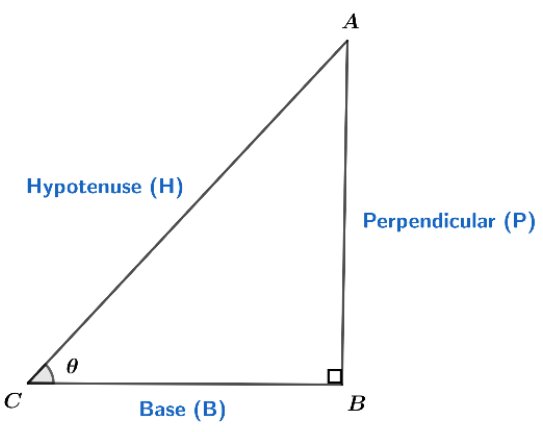
So,
$\Rightarrow $sin$\theta $ = $\dfrac{\text{perpendicular(P)}}{\text{hypotenuse(H)}}$
As we know that cosec$\theta $ is inverse of sin$\theta $.
$\Rightarrow $cosec$\theta $ = $\dfrac{\text{hypotenuse(H)}}{\text{perpendicular(P)}}$
Now, let’s see some even and odd functions.
$\Rightarrow $sin(-x) = -sinx
$\Rightarrow $ cos(-x) = cosx
$\Rightarrow $ tan(-x) = -tanx
$\Rightarrow $ cot(-x) = -cotx
$\Rightarrow $ cosec(-x) = -cosecx
$\Rightarrow $sec(-x) = secx
Let’s draw the graph now for the equation:
y = csc(x – 45)

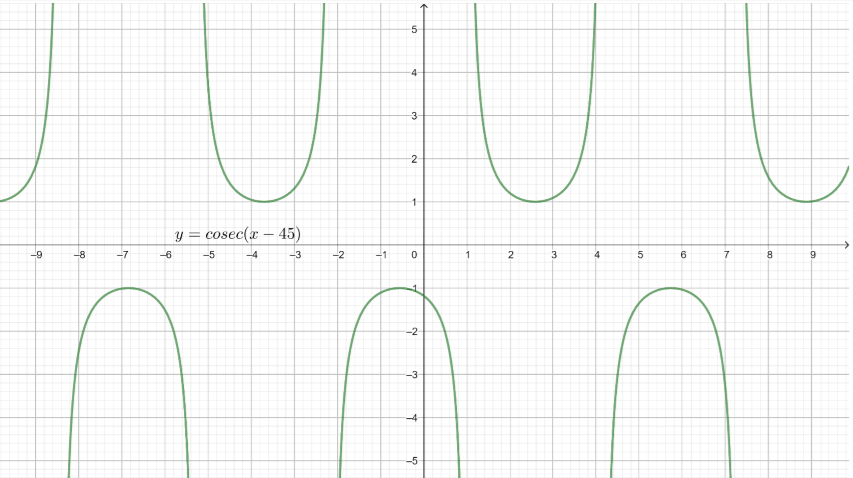
Note: Do mention the equation which you represented on the graph. And do sketch it neatly. You should know the basic trigonometric functions before solving anything related to the cosecant function.