Answer
Verified430.8k+ views
Hint: We are asked to solve the linear equation $9x+8y=15$ and $9x+8y=30$ .
To find the solution we will first find what are the possible ways to solve such a problem then after that we use our method to solve. We will find the value of ‘x’ and ‘y’ one by one. We will use graphical methods to understand different ways to solve our problem.
Complete step by step answer:
We are given a linear equation as $9x+8y=15$ and $9c+8y=30$ .We can see that our equations are linear and it has two variables ‘x’ and ‘y’ .So, it is a linear equation in two variables.
We have to find the solution to these two equations.
We know that, to find the solution of linear equation in two variables these are various way like –
1, Elimination method
2, Substitution method
3, Cross multiplication method
4, Graphical method
To find the solution, we can use any of the following and by each method we will always arise at the same
We will use elimination method in this we will eliminate any one of the variables and then solve for the remaining variables. To eliminate any variable, we will make their coefficient equal by multiplying the equation with the appropriate constant and then we add or subtract as required to eliminate. Once a variable is eliminated then we solve for another variable.
Now, we have $9x+8y=15$ ………………………………… (1)
And $9x+8y=30$ ……………………………….. (2)
We can see that the coefficient of ‘y’ in both the equations is same. So, we will eliminate ‘y’ here, as it will shorten our calculation.
Now, we subtract the equation (1) from equation (2) so, we get –
$\begin{align}
& 9x+8y=30 \\
& 9x+8y=15 \\
& -\text{ }-\text{ }- \\
& 0x+0y=15 \\
\end{align}$
Simplifying, we get –
$0=15$ .
Which is not true for any value of ‘x’ and ‘y’, so this equation has no solution.
If we try to eliminate the ‘x’ variable we will reach this equation only.
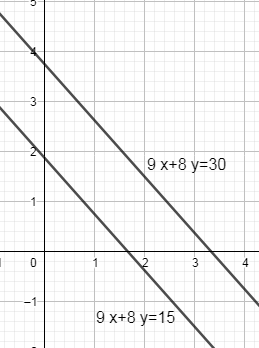
Note: If we look closely, we can see that the coefficient of ‘x’ and ‘y’ is the same in both the equation and the constant is different. If we draw a graph with these two equations, we will get that these two lines are parallel lines and we know two parallel lines have no solution because they do not intersect with each other at any point.
The solution is that point on the graph where two lines intersect.
To find the solution we will first find what are the possible ways to solve such a problem then after that we use our method to solve. We will find the value of ‘x’ and ‘y’ one by one. We will use graphical methods to understand different ways to solve our problem.
Complete step by step answer:
We are given a linear equation as $9x+8y=15$ and $9c+8y=30$ .We can see that our equations are linear and it has two variables ‘x’ and ‘y’ .So, it is a linear equation in two variables.
We have to find the solution to these two equations.
We know that, to find the solution of linear equation in two variables these are various way like –
1, Elimination method
2, Substitution method
3, Cross multiplication method
4, Graphical method
To find the solution, we can use any of the following and by each method we will always arise at the same
We will use elimination method in this we will eliminate any one of the variables and then solve for the remaining variables. To eliminate any variable, we will make their coefficient equal by multiplying the equation with the appropriate constant and then we add or subtract as required to eliminate. Once a variable is eliminated then we solve for another variable.
Now, we have $9x+8y=15$ ………………………………… (1)
And $9x+8y=30$ ……………………………….. (2)
We can see that the coefficient of ‘y’ in both the equations is same. So, we will eliminate ‘y’ here, as it will shorten our calculation.
Now, we subtract the equation (1) from equation (2) so, we get –
$\begin{align}
& 9x+8y=30 \\
& 9x+8y=15 \\
& -\text{ }-\text{ }- \\
& 0x+0y=15 \\
\end{align}$
Simplifying, we get –
$0=15$ .
Which is not true for any value of ‘x’ and ‘y’, so this equation has no solution.
If we try to eliminate the ‘x’ variable we will reach this equation only.
Note: If we look closely, we can see that the coefficient of ‘x’ and ‘y’ is the same in both the equation and the constant is different. If we draw a graph with these two equations, we will get that these two lines are parallel lines and we know two parallel lines have no solution because they do not intersect with each other at any point.
The solution is that point on the graph where two lines intersect.