Question

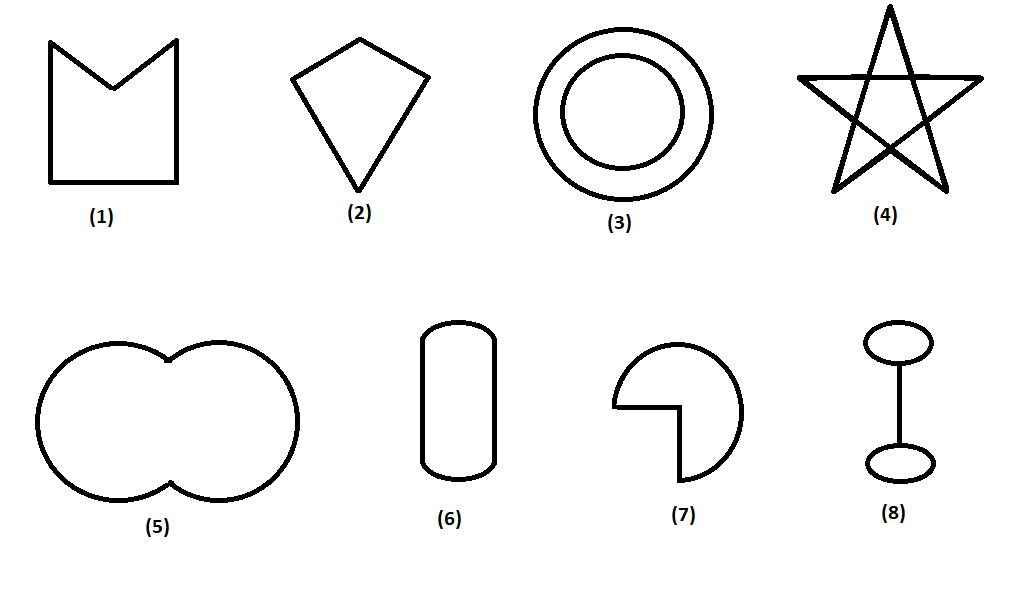
Identify the number of concave polygons from the given figures

A. 1
B. 2
C. 3
D. 4

Answer 1

Hint: First we’ll learn about the polygon and concave polygon than we’ll examine each figure individually whether they satisfy the conditions for the concave polygon or not.

Complete step by step answer:

A polygon is a figure made from a minimum of three line segments joining each other such that it made a closed figure.
Now, a concave polygon is a polygon consisting of at least one of the interior angles greater than $${180}^{\circ }$$, hence checking for the figures given.
1) If we see that it consist of line segments where the vertical angle is greater than $${180}^{\circ }$$, it is a concave polygon.
2) In this polygon, all the interior angles are less than $${180}^{\circ }$$, it is not a concave polygon.
3) This is a pair of a concentric circle, hence are not even polygon.
4) In this polygon, if we erase out the diagonals, the outer sides consist of a polygon where every alternate angle is greater than $${180}^{\circ }$$, it is a polygon.
5) In this figure we can see that it contains two arcs and is not even falling under the category of a polygon, hence are not even a polygon.
6) In this figure, the upper and lower part consists of two circular arcs, hence it is not a polygon or a concave polygon.
7) This figure also contains a circular arc that a polygon cannot have, hence it is not a polygon or a concave polygon.
8) This figure is not even a closed figure hence does not fall under either of the categories.
From the above results, we have 2 concave polygons.
Option (B) is correct.

Note: A polygon consists of only line segments so some student having a part as a curvature or arc thinks of the polygon which actually is not and also having figures like that if any angle comes out to be greater than mark them as concave polygon which is not, so keep this always in mind.