Question

If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.

Answer 1

Hint: First of all draw the diagram of information given in the question to visualize the same. Now use the corresponding angle theorem to prove the corresponding angles of two bisectors equal. Now use the converse of the corresponding angle theorem to prove two lines parallel.

Complete step-by-step answer:
Here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. Let us represent this situation diagrammatically.

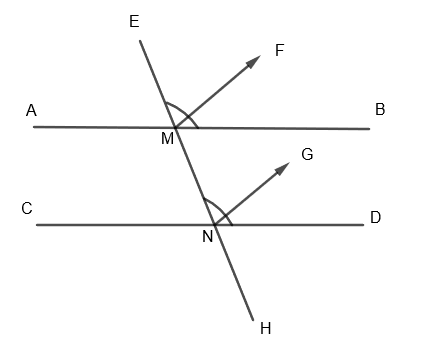
In the above diagram, the transversal EH intersects the two lines AB and CD at points M and N respectively. MF is the bisector of \[\angle EMB\] and NG is the bisector of \[\angle MND\]. We are given that MF and NG are parallel to each other. We have to prove that lines AB and CD are parallel. Here, as MF is the bisector of \[\angle EMB\], so we get,
\[\angle EMF=\dfrac{1}{2}\angle EMB.....\left( i \right)\]
 Also, NG is the bisector of \[\angle MND\], so we get,
\[\angle MNG=\dfrac{1}{2}\angle MND.....\left( ii \right)\]
Now by corresponding angle theorem, we know that, if two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. So here, since MF and NG are parallel and EH is the transversal, therefore, by corresponding angle theorem, we get,
\[\angle EMF=\angle MNG\]
By substituting the values of \[\angle EMF\] and \[\angle MNG\] from equation (i) and (ii), we get,
\[\angle EMB=\angle MND\]
Now by converse corresponding angle theorem, we know that, if two lines and a transversal form congruent corresponding angles, then the lines are parallel. So here, since corresponding angles \[\angle EMB\] and \[\angle MND\] are equal, So we get,
\[AB||CD\]
Hence we have proved that lines AB and CD are parallel to each other.

Note: Students are advised to remember the corresponding theorem and its converse as it is very useful in questions of geometry. Many students make a mistake while identifying the transversal of two lines and corresponding angles. So they must note that transversal is the line cutting two parallel lines and corresponding angles are angle between lines and transversal on the same side of it.