
If PQ be a normal chord of the parabola and if S be the focus, prove that the locus of the centroid of the triangle SPQ is curve
Answer
518.4k+ views
Hint- Always remember the equation of the normal chord. And put the values as
Complete Step-by-step answer:
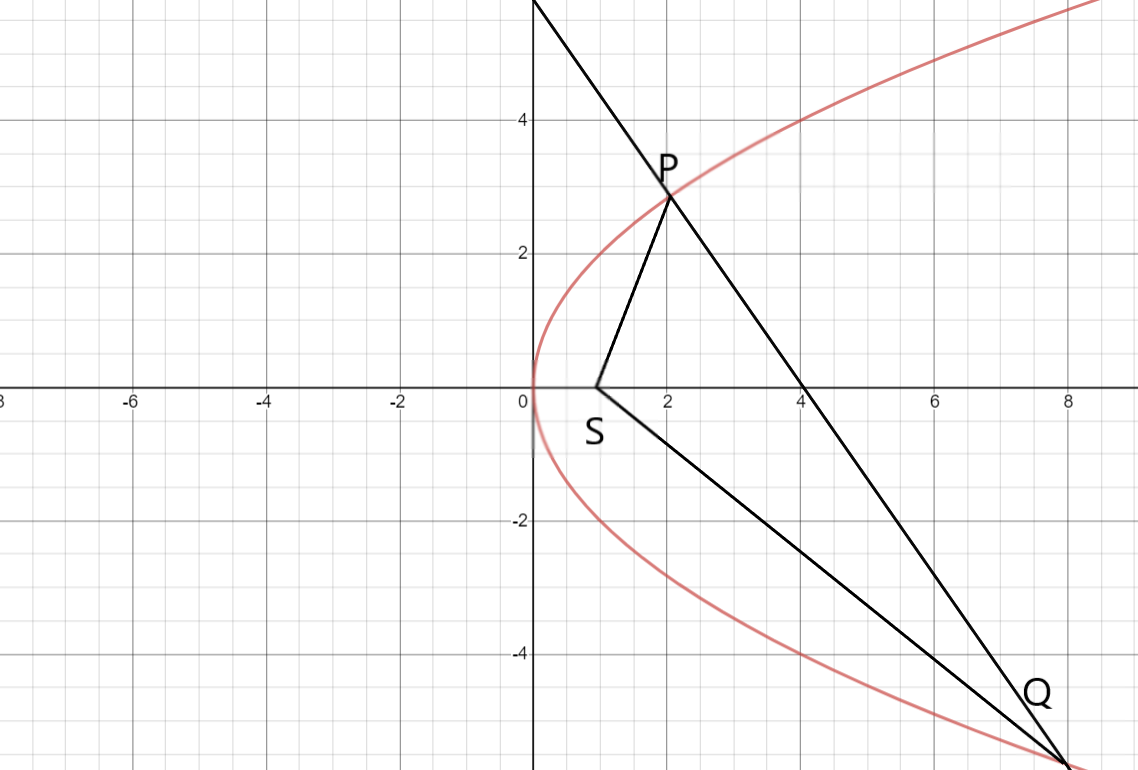
If the focus of the parabola is S, then the coordinates will be
As we all know, the equation of a parabola is
Let the equation of the normal chord at point P be
Then, the value of y will be-
Let the other point where it cuts be named Q, then the coordinates of the point Q will be
The relation here is-
The formula for the centroid of the triangle SPQ where the coordinates are
Now, as we know,
So,
Replacing
Hence proved.
Note: Use the equation of parabola in the starting of the question and pay special attention to the superscripts and subscripts as they are a wee but congested in these type of questions and mat completely vary your answer if not done in a right way.
Complete Step-by-step answer:

If the focus of the parabola is S, then the coordinates will be
As we all know, the equation of a parabola is
Let the equation of the normal chord at point P be
Then, the value of y will be-
Let the other point where it cuts be named Q, then the coordinates of the point Q will be
The relation here is-
The formula for the centroid of the triangle SPQ where the coordinates are
Now, as we know,
So,
Replacing
Hence proved.
Note: Use the equation of parabola in the starting of the question and pay special attention to the superscripts and subscripts as they are a wee but congested in these type of questions and mat completely vary your answer if not done in a right way.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




