Question

If the diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, then the kind of the quadrilateral is:
(a) a parallelogram with no angle equal to a right angle
(b) a rectangle
(c) a trapezium
(d) a scalene quadrilateral

Answer 1

Hint: Here, we need to find the kind of the given cyclic quadrilateral. We will use the property of an angle in a semi-circle to find the measures of the interior angles of the cyclic quadrilateral. Using the measures of the angles, we can determine the type of the quadrilateral.

Complete step-by-step answer:
First, we will draw the required figure for the problem.

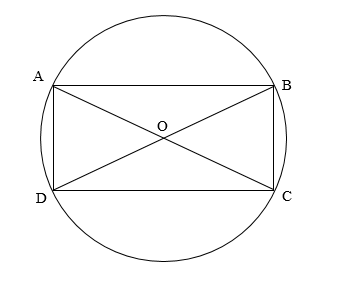
Here, O is the centre of the circle, AC and BD are the diameters of the circle, and the diagonals of the quadrilateral ABCD. ABCD is a cyclic quadrilateral.
Now, we can observe that the arc ADC and the diameter AC form a semi-circle.
The angle in a semi-circle is always a right angle. It is the angle formed by the diameter on any point on the semi-circle.
Therefore, we get
\[\angle ADC = 90^\circ \]
The arc ABC and the diameter AC form a semi-circle.
Therefore, we get
\[\angle ABC = 90^\circ \]
The arc BCD and the diameter BD form a semi-circle.
Therefore, we get
\[\angle BCD = 90^\circ \]
The arc BAD and the diameter BD form a semi-circle.
Therefore, we get
\[\angle BAD = 90^\circ \]
Therefore, in the cyclic quadrilateral ABCD, we have
\[\angle ADC = \angle ABC = \angle BDC = \angle BAD = 90^\circ \]
Since all the interior angles of the cyclic quadrilateral ABCD are right angles, the cyclic quadrilateral ABCD is a rectangle.
Thus, the correct option is option (b).
Note: The quadrilateral given in the question is a cyclic quadrilateral. A cyclic quadrilateral is that quadrilateral whose four vertices lie on a circle. The opposite interior angles of a cyclic quadrilateral are supplementary angles. In other words, the sum of the opposite interior angles of a cyclic quadrilateral is 180 degrees.