Question

If the length of a diagonal of a square is 8 cm. then find the length of the side of the square.

Answer 1

Hint:
We can draw a square with a diagonal and label it. Then we can find a right-angled triangle with the diagonal as the hypotenuse. Then we can apply Pythagoras theorem to get an equation relating the side of the square and diagonal. Then we can substitute the given value of diagonal and solve the equation to get the required length of the side of the square.

Complete step by step solution:
We can draw a square ABCD with a side a cm and diagonal AC with 8cm.

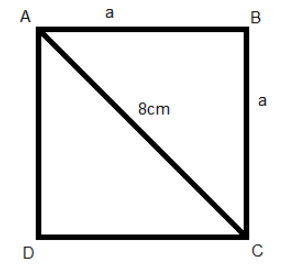
We know that for a square all the angles will be right angles.
So, we can say that triangle ABC is a right angles triangle.
We know that, by Pythagoras theorem, the sum of the squares of the non-hypotenuse sides is equal to the square of the hypotenuse. On applying this condition in the triangle ABC, we get,
 $ \Rightarrow A{C^2} = A{B^2} + B{C^2}$
Now we can substitute the values,
 $ \Rightarrow {8^2} = {a^2} + {a^2}$
On simplification, we get,
 $ \Rightarrow 64 = 2{a^2}$
On dividing throughout with 2, we get,
 $ \Rightarrow {a^2} = 32$
Now we can take the positive square root,
 $ \Rightarrow a = \sqrt {32} $
We can factorise the terms inside the root.
 $ \Rightarrow a = \sqrt {2 \times 2 \times 2 \times 2 \times 2} $
 $ \Rightarrow a = 2 \times 2\sqrt 2 $
 $ \Rightarrow a = 4\sqrt 2 $

So, the length of the side of the square with diagonal 8cm is $4\sqrt 2 cm$ .

Note:
Alternate solution to the problem is given by,

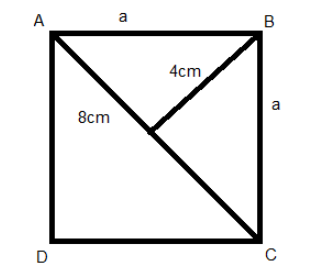
We know that the diagonal of a square will divide the square into two triangles of equal area and the diagonal are the perpendicular bisectors of each other.
So, we can write the area of triangle ABC in 2 ways,
 $A = \dfrac{1}{2}bh$
 $ \Rightarrow A = \dfrac{1}{2} \times 8 \times 4$
 $ \Rightarrow A = 16c{m^2}$
As the triangle is right angled at B, we can write the area in terms of a.
 $A = \dfrac{1}{2}bh$
 $ \Rightarrow A = \dfrac{1}{2} \times a \times a$
 $ \Rightarrow A = \dfrac{1}{2}{a^2}c{m^2}$
On equating the area, we get,
 $ \Rightarrow 16 = \dfrac{1}{2}{a^2}$
 $ \Rightarrow {a^2} = 32$
Now we can take the positive square root,
 $ \Rightarrow a = \sqrt {32} $
 $ \Rightarrow a = 4\sqrt 2 $
So, the length of the side of the square with diagonal 8cm is $4\sqrt 2 cm$ .