Question

If the sides of a triangle are in the ratio $3:4:5$, prove that it is a right-angled triangle.

Answer 1

Hint: In order to prove that the triangle is a right-angled triangle or not, take the ratio as the length of the sides then consider the triangle to be a right-angled triangle, then prove the Pythagoras theorem. If the sides satisfy the Pythagoras theorem, then it’s a right-angled triangle otherwise, it’s not a right-angled triangle.

Complete step by step solution:
We are given the sides of a triangle whose ratio is $3:4:5$.
Considering the sides to be $3x,4x,5x$.
Since, we know that the length of hypotenuse is always greater than the other two sides, so we are taking the hypotenuse to be $5x$ and other remaining sides to be $3x$ and $4x$.
Let’s make a rough diagram of a triangle ABC, whose sides are $3x$ and $4x$, and whose hypotenuse is $5x$.

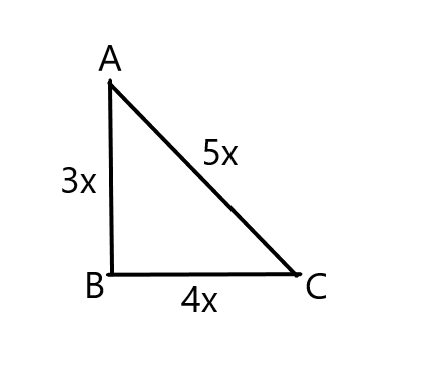
We are only considering that the given triangle is a right-angled triangle. For that we need to prove that the sides follow Pythagoras theorem.
So, for Pythagora's theorem, we know that the sum of the square of the base side and square of the height side is equal to the square of the hypotenuse.
Squaring the base side $4x$, we get:
${\left( {4x} \right)^2} = 16{x^2}$ …….(1)
Similarly, squaring the height side $3x$, we get:
${\left( {3x} \right)^2} = 9{x^2}$ …….(2)
Squaring the hypotenuse side $5x$, and we get:
${\left( {5x} \right)^2} = 25{x^2}$ …….(3)
Taking the sum of (1) and (2):
$16{x^2} + 9{x^2} = 25{x^2}$, which is equal to the equation (3).
That means the sum of the square of base and the square of height is equal to the square of hypotenuse, that satisfies the Pythagoras theorem, that implies the triangle ABC is actually a right-angled triangle, which is right-angled at B. And this proves our consideration to be true.
Therefore, ‘Yes’ the triangle having sides in ratio $3:4:5$ is a right-angled triangle.

Note:
> Pythagora's theorem is always applied on the right-angled triangle, we cannot apply it on any other triangle.
> Right-angled triangle is a triangle whose one side is ${90^ \circ }$ and rest angles are acute angles.